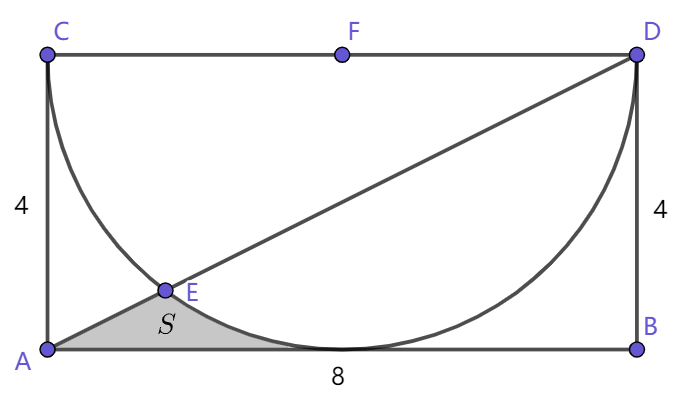
最近,网上流传这样一道据说是小学六年级的数学题:
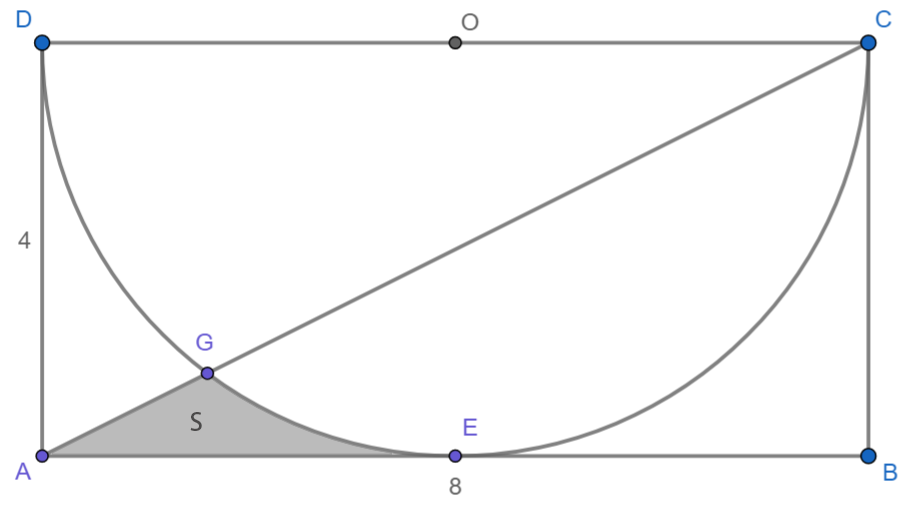
如下图,矩形的长和宽分别为8和4,求阴影部分$S$的面积。
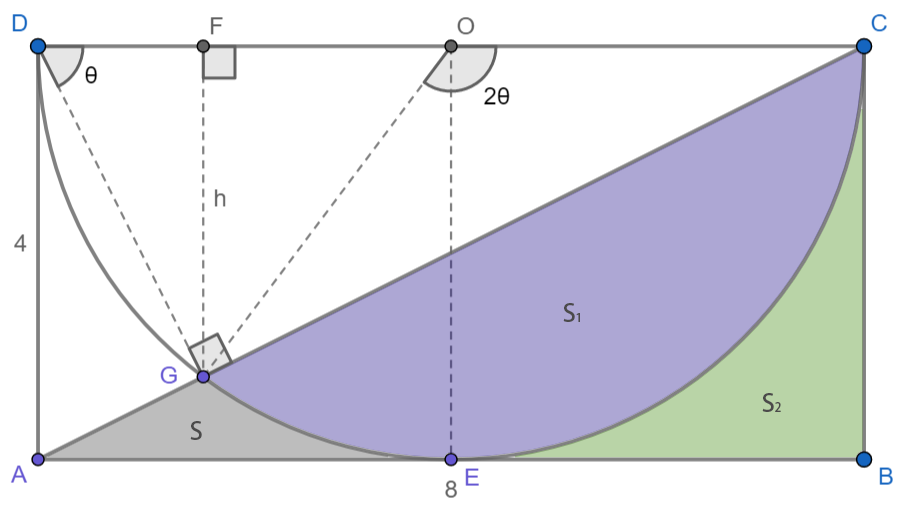
作图:连结DG,FG,OG,过点G向CD做垂线GF。
显然有:DG⊥GC,∠CAD=∠GDC=θ=arctan 2,∠GOC=2θ,h=16/5
$$\begin{aligned}
S_{ΔABC}&=\frac{1}{2}\times 8 \times 4=16 \,\text{(三角形面积)}\\
S_1&=4\times 4-\frac{1}{4}\pi 4^2 \,\text{(正方形面积减去四分之一个圆的面积)}\\
S_2&=(2\theta)\frac{4^2}{2}-\frac{4h}{2} \,\text{(扇形面积减去三角形面积)}
\end{aligned}$$
所以,所求阴影部分面积为:
$$\begin{aligned}
S&=S_{ΔABC}-S_1-S_2\\
&={\color{Blue}{\frac{32}{5}+4\pi-16\arctan 2}}
\end{aligned}$$
从结果来看,这并不是一道只具备我国小学知识就可以解决的问题。
结合Mathematica计算的结果:$\frac{32}{5}-8 \arcsin \frac{3}{5}$(计算方法参见评论),感觉应该会有更简洁的方法才对,于是尝试了一下,找到下面这种方法,虽然称不上优美,但也算简洁。
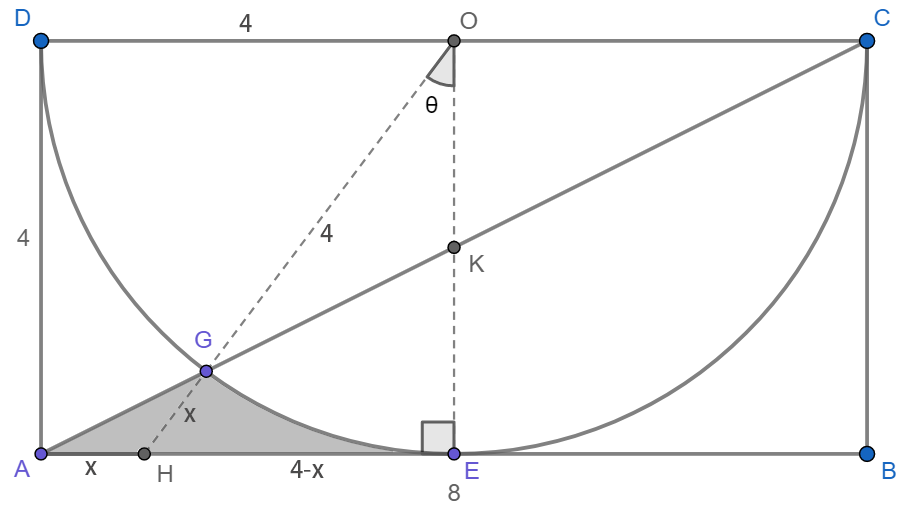
如上图,连结OG并延长交AB与H,连结点O与切点E交线段AC与点K。
因为 AB//CD
所以 ∠BAC=∠ACD
又由于 ∠ACD=∠OGC=∠AGH
所以 ∠HAG=AGH
所以设 x=AH=HG
所以有 HF=4-x
由勾股定理:$(4-x)^2+4^2=(4+x)^2$
解得 x=1,所以 $\theta=∠GOE=\arcsin \frac{3}{5}$
所以阴影部分面积等于$S_{ΔAEK}-S_{扇OGE}+S_{ΔOGK}={\color{Blue}{\frac{32}{5}-8 \arcsin \frac{3}{5}}}$
