用Mma给吉他调音

前几日网购一入门吉他，玩了几天后，音便不准了。
于是又买了个电子调音器，确实好用，但却花掉20来块钱。
日后，用Mma写了段调音的代码，在此与大家分享，希望能为您省下这几十元。

一、乐理知识

初中物理中就已经指出，音调的高低与发声物体的振动频率有关，频率越高音调越高。下面简单介绍下十二平均律。
将八度分成12个相等的部分（半音）的音律叫作十二平均律，它们构成了7个基本音级，详见下表：

音级	频率(Hz)	唱名简谱	公式
C4	261.626	1	$440\times {{2}^{-9/12}}$
C4♯	277.183	1#	$440\times {{2}^{-8/12}}$
D4	293.665	2	$440\times {{2}^{-7/12}}$
D4♯	311.127	2#	$440\times {{2}^{-6/12}}$
E4	329.628	3	$440\times {{2}^{-5/12}}$
F4	349.228	4	$440\times {{2}^{-4/12}}$
F4♯	369.994	4#	$440\times {{2}^{-3/12}}$
G4	391.995	5	$440\times {{2}^{-2/12}}$
G4♯	415.305	5#	$440\times {{2}^{-1/12}}$
A4	440	6	$440\times {{2}^{0}}$
A4♯	466.164	6#	$440\times {{2}^{1/12}}$
B4	493.883	7	$440\times {{2}^{2/12}}$

然而仅仅这12个音级还远远不够，于是，在音级后用数字加以区分。
表达方法主要有两种，分别是：科学记音法和亥姆霍兹记音法，对照如下：

科学记音法	亥姆霍兹记音法	频率 (Hz)	频率计算 (Hz)
A9	a”””	14080	$440\times {{2}^{5}}$
A8	a””’	7040	$440\times {{2}^{4}}$
A7	a””	3520	$440\times {{2}^{3}}$
A6	a”’	1760	$440\times {{2}^{2}}$
A5	a”	880	$440\times {{2}^{1}}$
A4	a′	440	$440\times {{2}^{0}}$
A3	a	220	$440\times {{2}^{-1}}$
A2	A	110	$440\times {{2}^{-2}}$
A1	A͵或͵A	55	$440\times {{2}^{-3}}$
A0	A͵͵或͵͵A	27.5	$440\times {{2}^{-4}}$
A−1	A͵͵͵或͵͵͵A	13.75	$440\times {{2}^{-5}}$

吉他六根弦的音级与频率如下表所示：

表1 吉他各弦音级与频谱

吉它弦→	6弦	5弦	4弦	3弦	2弦	1弦
科学记音法→	E2	A2	D3	G3	B3	E4
频率→	82.407	110.000	146.832	195.998	246.942	329.628
频率→	$440\times 2^{-29/12}$	$440\times 2^{-24/12}$	$440\times 2^{-19/12}$	$440\times 2^{-14/12}$	$440\times 2^{-10/12}$	$440\times 2^{-5/12}$

吉他与钢琴音级对照如下：

二、关于泛音

纯音：仅有单一频率的声音。
泛音：有多种频率的声音，且每种频率都是其最小频率的整数倍。
泛音中频率最小的频率称为基频（即我们确定音调的频率），对应的声音称为基音，其它的都称为泛音（可依次命名为：一泛音，二泛音，…）。
泛音是影响音色的主要因素，从泛音的比例大致可以推出声音来自何种乐器，或通过泛音来合成电子乐器。
在自然界中，几乎所有的声音都不是纯音，因此我们可以区分不同的发音器具。
纯音可以通过音叉和软件方式产生。
泛音的产生原理，可以通过弦在振动时产生的驻波现象理解。
由于泛音的存在，给我们识别基频带来的难度，不过这也提供了一种验证方式——去掉基频及其泛音时，频谱能量骤减，但将基频的一半或三分一、四分之一等作为假定基频时，也有会使频谱能量骤减。因此我们要找最大的那个假定基步作为真正的基频。

三、用Mma为吉他调音

3.1、函数介绍

Fourier：离散傅里叶变换。
FindClusters：聚类。
Ordering：返回列表的顺序。
SystemDialogInput[“RecordSound”]：打开系统录音工具，捕获音频。
SystemDialogInput[“FileOpen”]：选择文件路径。
对于WAV文件支持导入的元素：Audio, AudioChannels, AudioEncoding, AudioFile, Data, Duration, Length, MetaInformation, SampleDepth, SampledSoundList, SampleRate, Sound。

3.2、分步处理过程

3.2.1、定义常量

pinlv=Reverse[440.0 2^(#/12)&/@{-29,-24,-19,-14,-10,-5}];(*吉他六根弦的频率*)
names=Reverse[{"音级：E2(6弦)","音级：A2(5弦)","音级：D3(4弦)","音级：G3(3弦)","音级：B3(2弦)","音级：E4(1弦)"}];(*吉他六根弦的名称*)
guitar=Thread[pinlv->names];

3.2.2、导入数据

path = SystemDialogInput["FileOpen"];(* 指定文件路径 *)
audioData = Import[path, "Data"];(* 导入数据 *)
(*au=SystemDialogInput["RecordSound"];*)(* 通过麦克风采集数据，请选择单声道：mono *)
audioDuration = Import[path, "Duration"];(* 录音时长 *)
(*audioSampleRate=Import[path,"SampleRate"];*)(* 采样率 *)
audioLength = Import[path, "Length"];(* 采样点数 *)

3.2.3、傅里叶变换

audioFrequency = Abs[Fourier[audioData]];(*傅里叶变换，频域信息*)
audioFrequency=audioFrequency[[;;Floor[audioLength/2]]](*由于傅里叶变换对称，仅取一半，实际可以取得更少*);
boundary=Mean[audioFrequency]+5StandardDeviation[audioFrequency];(*阈值，用于提到特征信息时使用*)
dataForAnalysis=Flatten[Position[audioFrequency,x_/;x>boundary]];(*过滤噪音，根据上面的阈值提取位置*)
dataForAnalysis={(#-1)/audioDuration,audioFrequency[[#]]}&/@dataForAnalysis;(* n 行 2 列的数据：真实频率频率（减1后除以时长），频率对应的能量*)
dataForAnalysis=Select[dataForAnalysis,#[[1]]>10&];(*舍弃小于等于10的频率*)
ListLinePlot[dataForAnalysis,PlotRange->{{0,All},All},Mesh->All,ImageSize->500](* 绘图：频率，能量*)

3.2.4、处理泛音，识别基音

overtone=FindClusters[dataForAnalysis[[;;,1]],Method->"NeighborhoodContraction"];(*聚类，每类为一个泛音*)
overtone=Flatten[Table[If[Length[overtone[[k]]]>1&&StandardDeviation[overtone[[k]]]>3,
FindClusters[overtone[[k]],Method->"NeighborhoodContraction"],
{overtone[[k]]}
],{k,Length[overtone]}],1];(*拆分较大的类*)
fundamentalFrequency=Mean[SortBy[overtone,Mean][[1]]];(*泛音最小的那一类，既为基音频率*)

3.2.5、输出表格


generateOvertone=fundamentalFrequency Range[20];(*根据基音频率生成泛音*)
diff=Min[(#-generateOvertone)^2]&/@dataForAnalysis[[;;,1]];(*误差的平方*)
mse=Mean[diff];(*均方误差*)
string=First[Nearest[guitar,fundamentalFrequency]];(*对应于哪根弦*)
error=fundamentalFrequency-First[Nearest[pinlv,fundamentalFrequency]];(*与应对的弦的误差*)
Grid[Prepend[{
{"基音频率",Row[{fundamentalFrequency,"Hz"}]},
{"最可能的弦",string},
{"误差",Row[{error,"Hz"}]},
{"建议",If[error>0,"如果您在调"<>StringTake[string,{-3,-2}]<>"，请调低些","如果您在调"<>StringTake[string,{-3,-2}]<>"，请调高些"]},
{"均方误差",mse}},{"名称","值"}],
Background->{None,{Lighter[Yellow,.9],{White,Lighter[Blend[{Blue,Green}],.8]}}},Dividers->{{Darker[Gray,.6],{Lighter[Gray,.5]},Darker[Gray,.6]},{Darker[Gray,.6],Darker[Gray,.6],{False},Darker[Gray,.6]}},
Alignment->{{Center,Center,{Left}}},
ItemSize->{{10,15}},
Frame->Darker[Gray,.6],
ItemStyle->14,
Spacings->{Automatic,.8}]

3.2.5、全部代码与输出结果

(* 定义常量 *)
pinlv=Reverse[440.0 2^(#/12)&/@{-29,-24,-19,-14,-10,-5}];(*吉他六根弦的频率*)
names=Reverse[{"音级：E2(6弦)","音级：A2(5弦)","音级：D3(4弦)","音级：G3(3弦)","音级：B3(2弦)","音级：E4(1弦)"}];(*吉他六根弦的名称*)
guitar=Thread[pinlv->names];

(* 导入数据 *)
path=SystemDialogInput["FileOpen"];(* 指定文件路径 *)
audioData=Import[path,"Data"];(* 导入数据 *)
(*au=SystemDialogInput["RecordSound"];*)(* 通过麦克风采集数据，请选择单声道：mono *)
audioDuration=Import[path,"Duration"];(* 录音时长 *)
(*audioSampleRate=Import[path,"SampleRate"];*)(* 采样率 *)
audioLength=Import[path,"Length"];(* 采样点数 *)

(* 傅里叶变换 *)
audioFrequency = Abs[Fourier[audioData]];(*傅里叶变换，频域信息*)
audioFrequency=audioFrequency[[;;Floor[audioLength/2]]](*由于傅里叶变换对称，仅取一半，实际可以取得更少*);
boundary=Mean[audioFrequency]+5StandardDeviation[audioFrequency];(*阈值，用于提到特征信息时使用*)
dataForAnalysis=Flatten[Position[audioFrequency,x_/;x>boundary]];(*过滤噪音，根据上面的阈值提取位置*)
dataForAnalysis={(#-1)/audioDuration,audioFrequency[[#]]}&/@dataForAnalysis;(* n 行 2 列的数据：真实频率频率（减1后除以时长），频率对应的能量*)
dataForAnalysis=Select[dataForAnalysis,#[[1]]>10&];(*舍弃小于等于10的频率*)
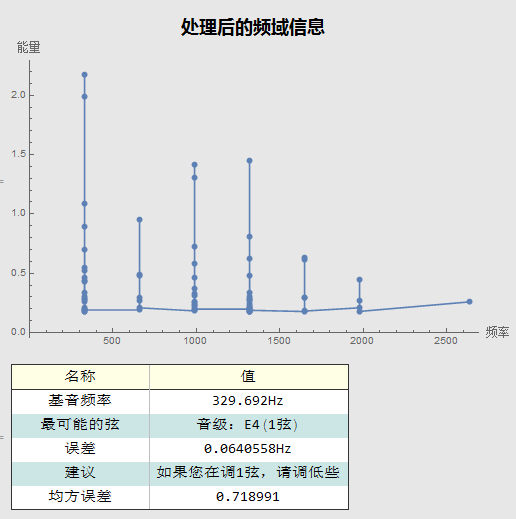
ListLinePlot[dataForAnalysis,PlotRange->{{0,All},All},Mesh->All,ImageSize->500,PlotLabel->Style["处理后的频域信息",18,Bold,Black,FontFamily->"微软雅黑"],AxesLabel->(Style[#,12]&/@{"频率","能量"})](* 绘图：频率，能量*)

(* 处理泛音，识别基音 *)
overtone=FindClusters[dataForAnalysis[[;;,1]],Method->"NeighborhoodContraction"];(*聚类，每类为一个泛音*)
overtone=Flatten[Table[If[Length[overtone[[k]]]>1&&StandardDeviation[overtone[[k]]]>3,
FindClusters[overtone[[k]],Method->"NeighborhoodContraction"],
{overtone[[k]]}
],{k,Length[overtone]}],1];(*拆分较大的类*)
fundamentalFrequency=Mean[SortBy[overtone,Mean][[1]]];(*泛音最小的那一类，既为基音频率*)

(* 输出表格 *)
generateOvertone=fundamentalFrequency Range[20];(*根据基音频率生成泛音*)
diff=Min[(#-generateOvertone)^2]&/@dataForAnalysis[[;;,1]];(*误差的平方*)
mse=Mean[diff];(*均方误差*)
string=First[Nearest[guitar,fundamentalFrequency]];(*对应于哪根弦*)
error=fundamentalFrequency-First[Nearest[pinlv,fundamentalFrequency]];(*与应对的弦的误差*)
Grid[Prepend[{
{"基音频率",Row[{fundamentalFrequency,"Hz"}]},
{"最可能的弦",string},
{"误差",Row[{error,"Hz"}]},
{"建议",If[error>0,"如果您在调"<>StringTake[string,{-3,-2}]<>"，请调低些","如果您在调"<>StringTake[string,{-3,-2}]<>"，请调高些"]},
{"均方误差",mse}},{"名称","值"}],
Background->{None,{Lighter[Yellow,.9],{White,Lighter[Blend[{Blue,Green}],.8]}}},Dividers->{{Darker[Gray,.6],{Lighter[Gray,.5]},Darker[Gray,.6]},{Darker[Gray,.6],Darker[Gray,.6],{False},Darker[Gray,.6]}},
Alignment->{{Center,Center,{Left}}},
ItemSize->{{10,15}},
Frame->Darker[Gray,.6],
ItemStyle->14,
Spacings->{Automatic,.8}]

下载测试文件

我录制的吉他6根弦的音频文件及 Mathematica 文件
百度网盘：链接：http://pan.baidu.com/s/1i53LbzZ 密码：lr1f

更新日期：2017-05-13