
一、题目介绍与假设
【原题目】
来自《75道逻辑思维题》第34题:
一个巨大的圆形水池,周围布满了老鼠洞。
猫追老鼠到水池边,老鼠未来得及进洞就掉入水池里。
猫继续沿水池边缘企图捉住老鼠(猫不能下水)。
已知两者速度的关系为:$v_\text{猫}=4v_\text{鼠}$(老鼠的最大速度是猫的四分之一)。
问老鼠是否有办法摆脱猫的追逐?
【假设】 为简单起见,不妨设:
①猫鼠都为无大小和形状的点;
②初始时猫位于水池正右侧岸边,老鼠位于圆心;
③当猫鼠恰好同时到达岸边时,老鼠可以逃入老鼠洞(即猫不能在岸边等待老鼠);
④水池半径$R=1 m$,猫鼠的最大速度分别为$v_\text{猫}=4 m/s$、$v_\text{鼠}=1 m/s$;
⑤猫总是尽全力保持与老鼠的距离最小;
⑥当老鼠、圆心、猫三点共线时(猫鼠在圆心两侧)猫总是向逆时针方向追逐老鼠。
二、逃脱方法
下面分别介绍我想到的3种逃脱方法:
- 方法一:最容易想到(只需要知道圆周长的计算公式);
- 方法二:用了些数学技巧(微分方程);
- 方法二:进一步优化方法二,也许是时间最短的逃脱方法了。
2.1 方法一:一种简单的逃脱方法
首先,老鼠径直游向岸边是不行的。因为,老鼠需要游一个半径的路径,用时$R/v_\text{鼠}=1 s$;而猫到达圆周任意一点最多只需要跑半个圆周,用时$\pi R/v_\text{猫}=\pi/4 \approx 0.79 s$。
通过上面的计算,虽然老鼠未能逃脱,但可以发现,如果老鼠能够想办法在游到某个距离岸边小于等于的$\pi/4$位置时,将猫甩在圆心的另一侧,这时老鼠全力游向岸边就可以成功逃脱了。
由于老鼠的最大速度是猫的四分之一,所以当老鼠在距离圆心$R/4=1/4$的圆形区域内时,其角速度是可以超过猫的角速度的,于是便得到了下面的逃脱方法:
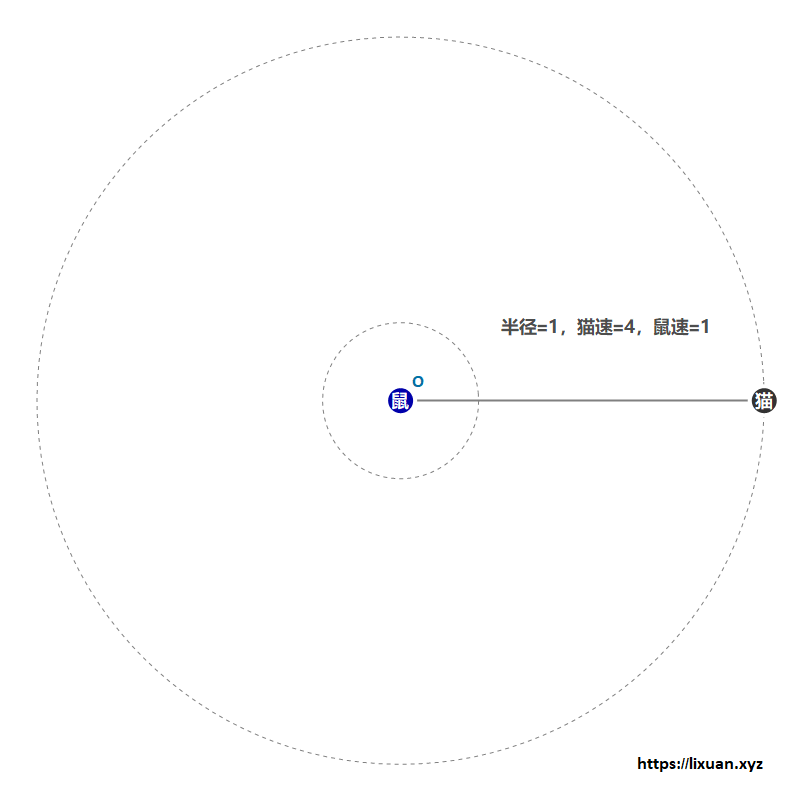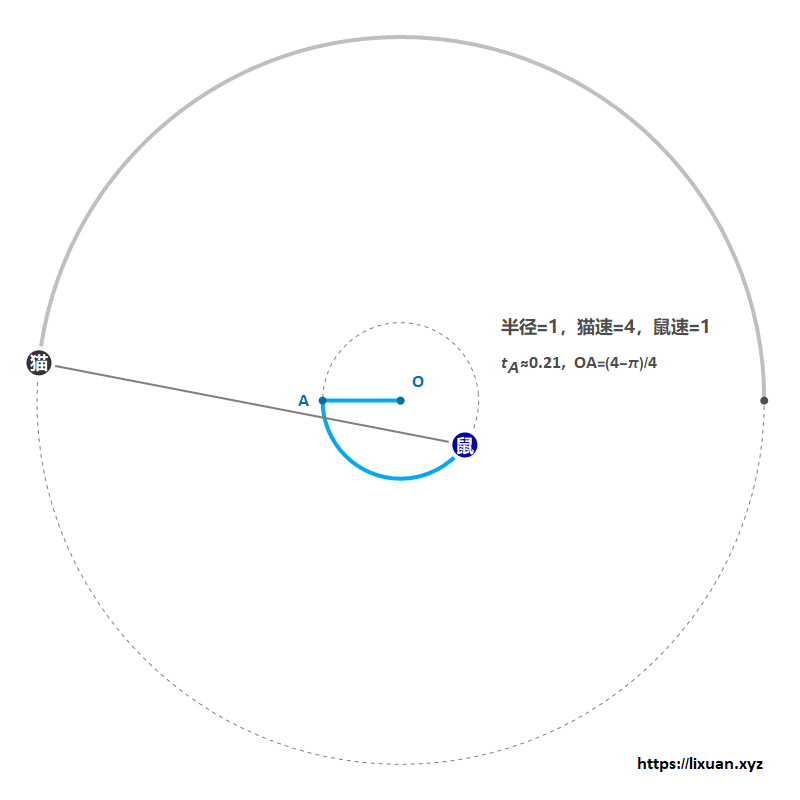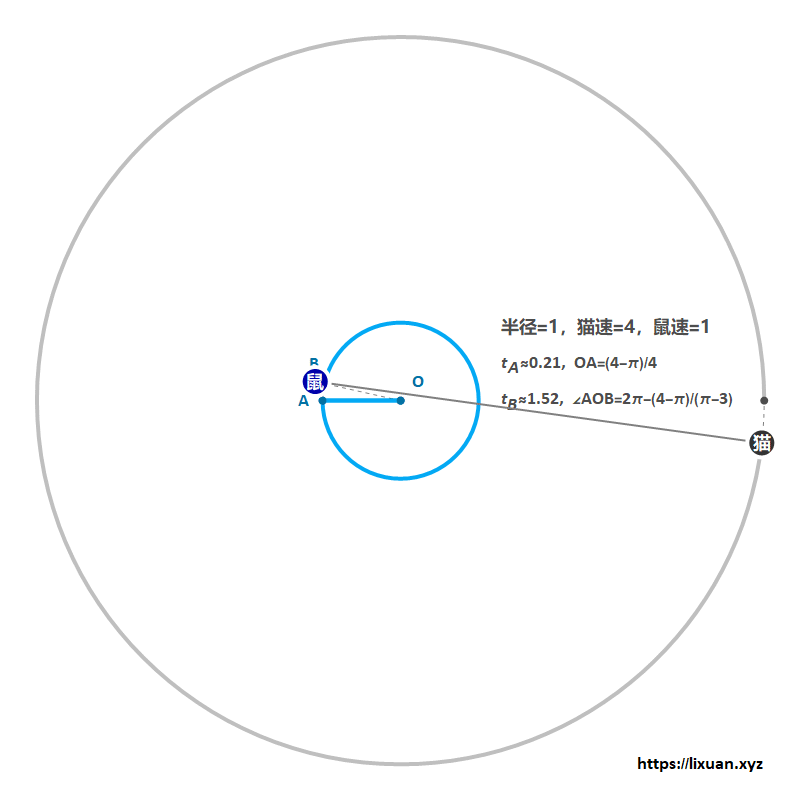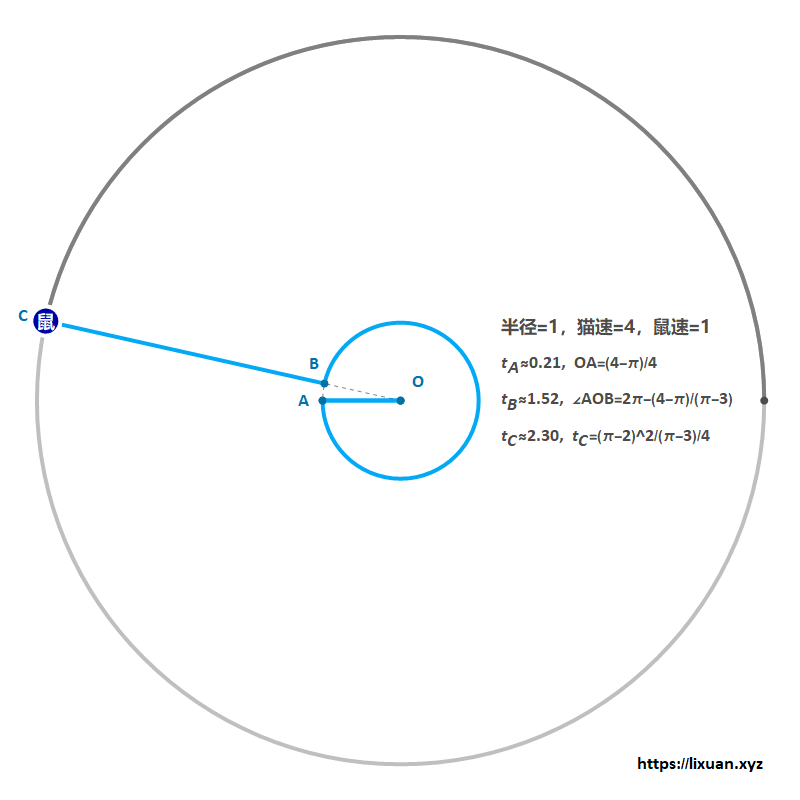
- 第一步:老鼠全速游到距离圆心$(4-\pi)R/4$处;
- 第二步:保持此距离,并全速绕圆心转圈,直至老鼠将猫甩得最远( 此时老鼠、圆心和猫共线 );
- 第三步:全速冲向最近的岸边即可成功逃脱(猫鼠恰好同时到达岸边)。
该方法最少需要$(\pi-2)^2/(\pi-3)/4\approx2.30$秒(由于老鼠一直以全速1 m/s 逃脱,所以在数值上距离和时间相等),参考图1:
2.2 方法二:探索最短时间
如果将方法一中的前两步合并定能缩短逃脱时间,即老鼠在离开圆心的同时将猫甩开。
假定猫鼠始终保持最大速度,具体逃脱方法:
- 第一步:老鼠保持与猫和圆心三点共线(圆心在两者中间,前面说过当老鼠在距离圆心$R/4$的圆形区域内时是可以办到的)全速远离圆心;
- 第二步:当老鼠到达可直线逃脱的位置(距离岸边3/4)时径直游向岸边即可。
对老鼠前半部分的逃脱策略,可以列出在极坐标下老鼠位置$(r,\theta)$的微分方程组:
$$
\left\{ \begin{align}
\frac{v_\text{猫}}{R}& =\frac{d\theta }{dt} &\text{(①:老鼠与猫保持角速度相同)}\\
v_\text{鼠}^{2}& = {{\left( \frac{dr}{dt} \right)}^{2}}+{{\left( r\frac{d\theta }{dt} \right)}^{2}}& \text{(②:老鼠一直以最大速度逃脱)}\
\end{align} \right. \tag{1}\label{1}
$$
初始条件:$r=0,\theta=\pi$,将①代入,并代入$v_\text{猫}=4 m/s$、$v_\text{鼠}=1 m/s$,得到:
$$
(\frac{dr}{dt})^2+16r^2=1 \tag{2}\label{2}
$$
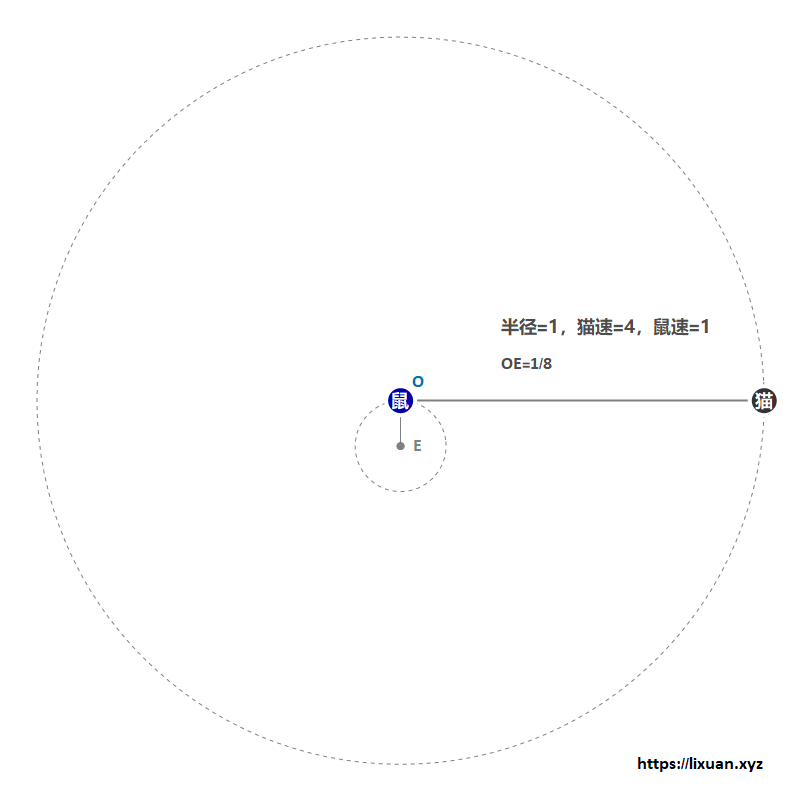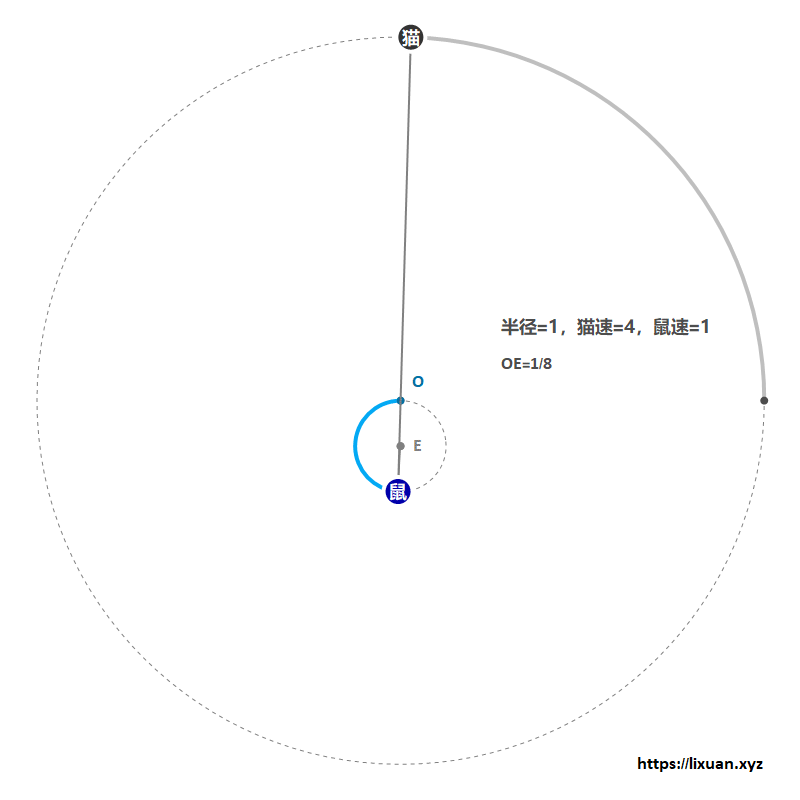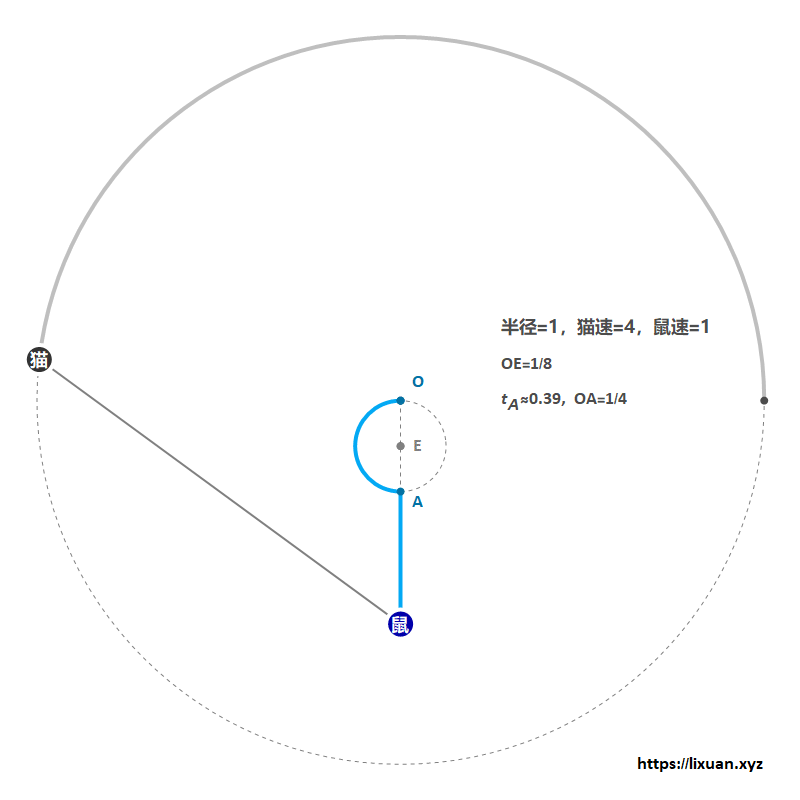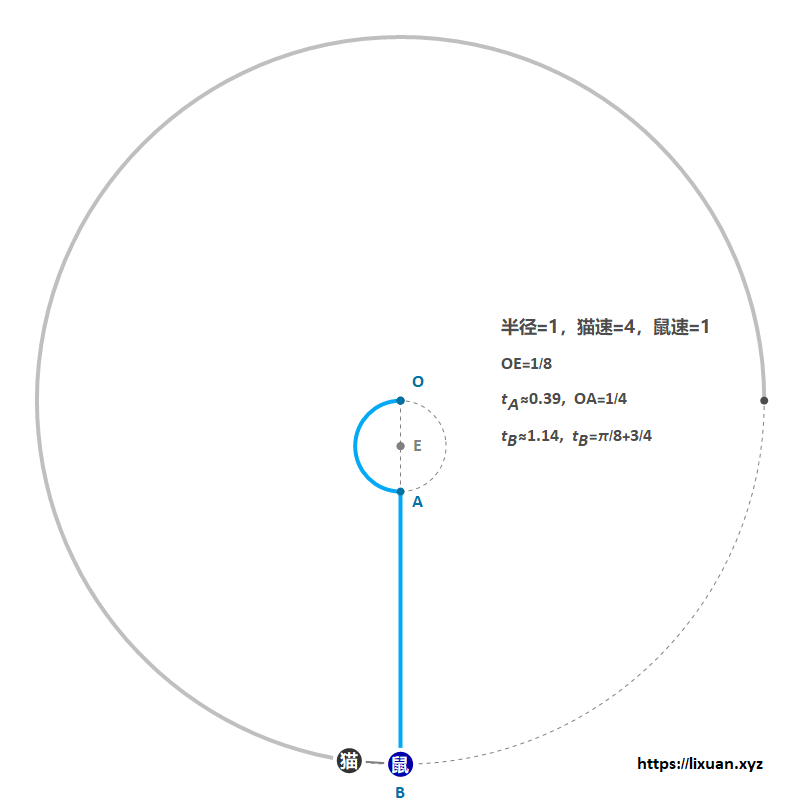
解得$r=\sin(4t)/4,\theta=4t+\pi$,即$r=\sin(\theta-\pi)/4$,这是一个以$(0,-1/8)$为圆心,以$1/8$为半径的圆。
该方法最少需要$\pi/8+3/4\approx 1.14$秒(由于老鼠一直以全速1 m/s 逃脱,所以在数值上距离和时间相等),参考图2:
2.3 方法三:对方法二的优化
方法二中,老鼠到达岸边时,猫还有一段距离才能赶到,可见方法二还有较大的优化空间。因此,在方法二的基础上,修改第二步,具体逃脱方法如下:
- 第一步:老鼠保持与猫和圆心三点共线(圆心在两者中间,前面说过当老鼠在距离圆心$R/4$的圆形区域内时是可以办到的)全速远离圆心;
- 第二步:老鼠不必游到距离岸边3/4处,在中途尽可能早的延当前切线方向跑向岸边。
下面计算第二步中的“尽可能早”,即当老鼠恰好能够逃脱时,猫鼠将会同时达到岸边(下图点B),此时猫的路程是老鼠的4倍。
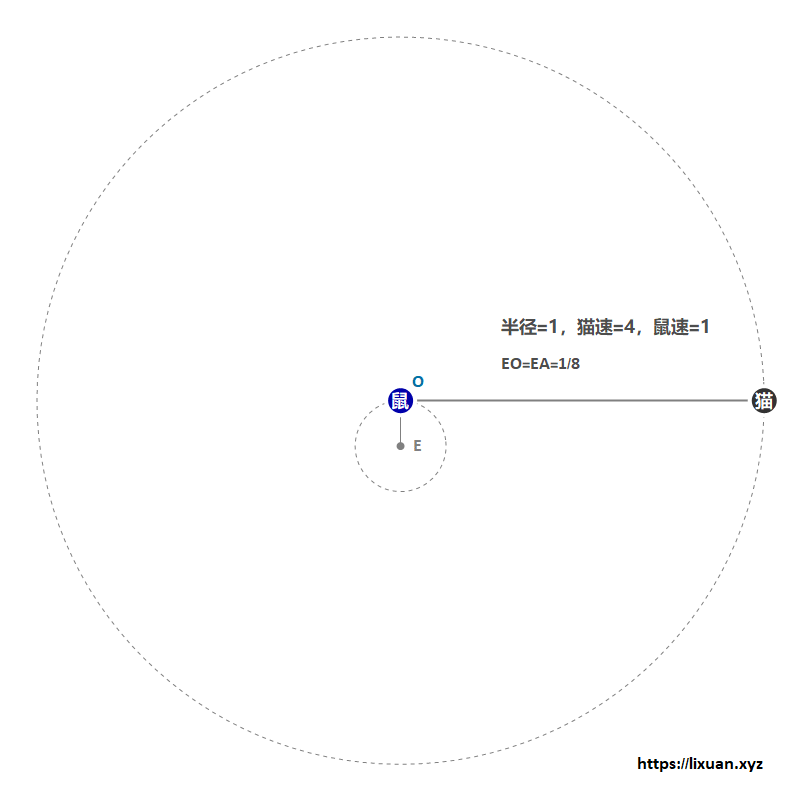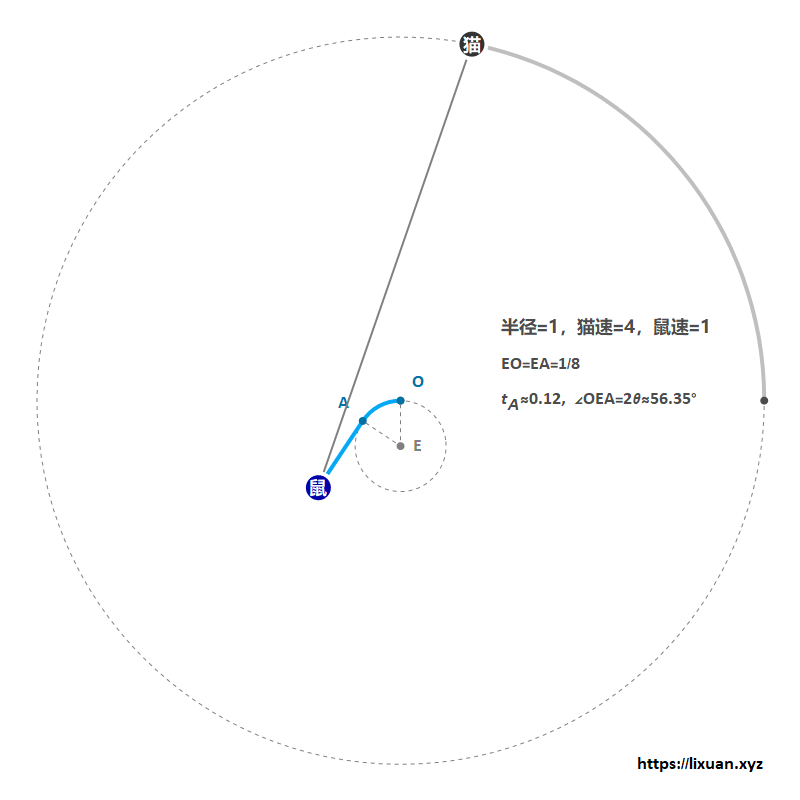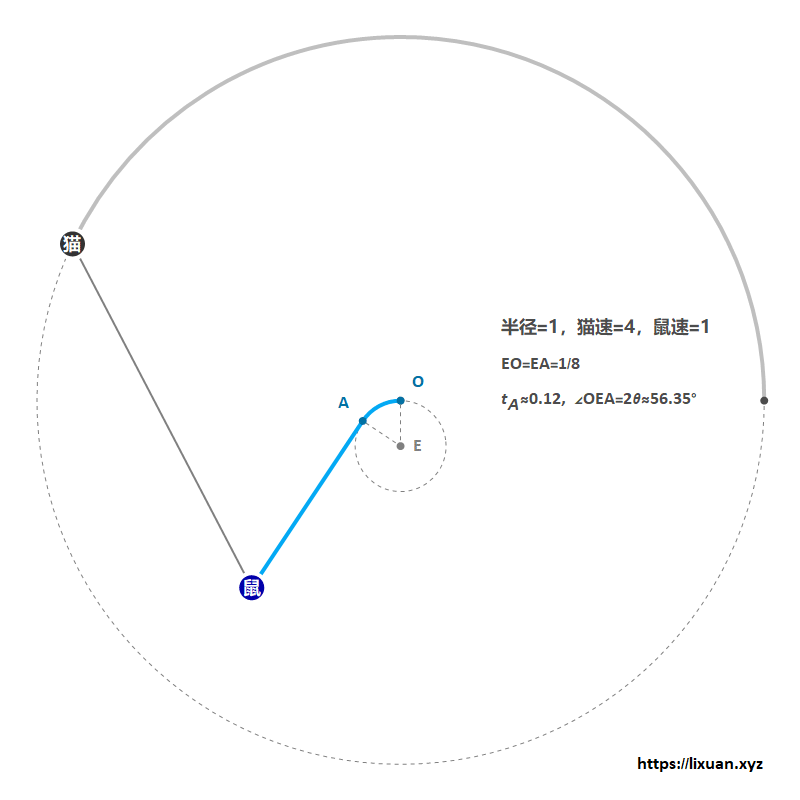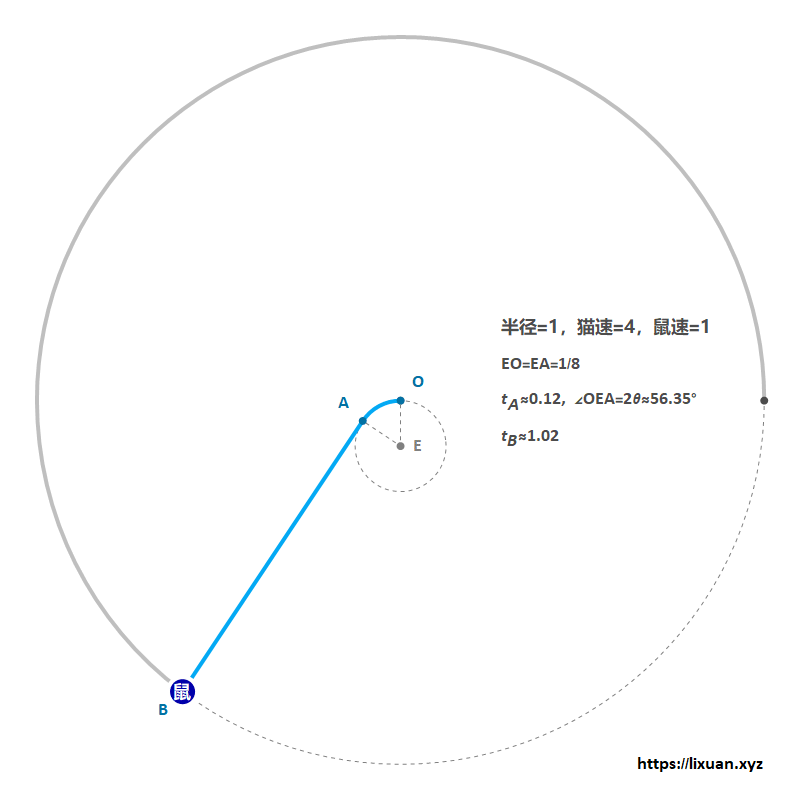
如下图(本来OE应该等于1/8,但为了方便展示,将图中OE取得更长一些),圆O的半径等于1,圆E的半径等于$1/8$,蓝色粗曲线是老鼠游过的轨迹(由一段半径为$1/8$的圆弧$\overset{\frown}{OA}$与切线$AB$组成),红色粗线是猫跑过的轨迹。
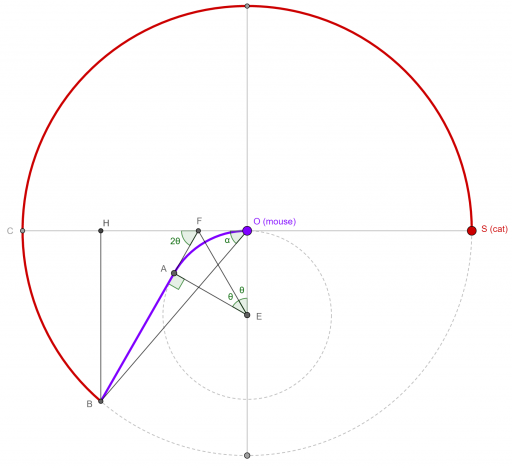
设$\angle OEA=2\theta$是老鼠在圆弧阶段游过的角度(显然$0<\theta<\frac{\pi}{2}$,后面化简用到时不再赘述),则有$\angle BFC=\angle OEA=2\theta$(同角的补角相等),连结EF,则有$\triangle EFA \cong \triangle EFO$。
设$\alpha+\pi$是猫跑过的角度,即$\angle BOC=\alpha$(显然$0<\alpha<\frac{\pi}{2}$,后面化简用到时不再赘述),由于半径等于1,所以$\alpha+\pi$也是猫跑过和路程。
于是由猫的路程是老鼠的4倍这一关系可以得到如下方程:
$$
\begin{aligned}
\alpha+\pi&=4(\overset{\frown}{OA}+AB)\\
&=4\left[\frac{1}{8}(2\theta)+BF-AF \right]\\
&=\theta+\frac{4\sin \alpha}{\sin 2\theta}-\frac{1}{2}\tan \theta
\end{aligned} \tag{3}\label{3}
$$
上面方程中有两个未知数:$\theta, \alpha$,所以还需要再找到它们的另一关系,如上图OF有两种表达方式(等号左边在$\triangle EOF$中,等号右边在$\triangle BHF$和$\triangle BHO$中):
$$
\begin{aligned}
\frac{1}{8}\tan \theta&=\cos \alpha – \frac{\sin \alpha}{\tan 2\theta}\\
&=\sqrt{1+\frac{1}{\tan^22\theta}}\cos(\alpha+\beta)\\
&=\frac{1}{\sin 2\theta}\cos(\alpha+\beta),\quad \text{这里}\beta=\arccos(\sin 2\theta)=\frac{\pi}{2}-2\theta
\end{aligned} \tag{4}\label{4}
$$
所以有:
$$
\begin{align}
\frac{1}{4}\sin^2\theta=\cos(\alpha+\frac{\pi}{2}-2\theta)
\end{align} \tag{5}\label{5}
$$
即:
$$\alpha=\arccos(\frac{\sin^2\theta}{4})+2\theta-\frac{\pi}{2} \tag{6}\label{6} $$
代入方程(3)得到:
$$
\arccos(\frac{\sin^2\theta}{4})+2\theta-\frac{\pi}{2}+\pi
=\theta+\frac{4\sin\left[\arccos(\frac{\sin^2\theta}{4})+2\theta-\frac{\pi}{2}\right]}{\sin 2\theta}-\frac{1}{2}\tan \theta \tag{7}\label{7}
$$
该方程过于复杂,这里只能计算其近似解了:$\theta\approx 0.491738$,$\alpha \approx 0.927714$。
进而计算出老鼠用时约为$1.01733$秒(由于老鼠一直以全速1 m/s 逃脱,所以在数值上距离和时间是相等的),参考图3:
2.4 方法三也许是时间最短的逃脱方法了
这类题更像是变分法的习题,但由于我学艺不精,没能把不等条件抽象成相等条件的变分问题,以后有时间再复习复习变分法知识,如果想通了再在此更新。
虽然没能使用变分法,但我猜这已经是老鼠在时间上的最优逃脱方法了。
如下图所示,还是在假定猫优先逆时针追逐老鼠,那么老鼠在时间上比方法三更优的路线必然在灰色的“更优区域”内,而且猫和老鼠同时到达岸边的位置$B’$也必然在弧$\overset{\frown}{BC}$上,同时老鼠为了节约时间,所以其最初的路线必然会在圆E上,然后沿切线游到点$B’$。这样一来,不正是方法三的思路么,而方法三计算的就是这个思路的最优路径呀。所以,我猜方法三已经是该问题在时间上的最优解了。

延伸
如果将该问题做如下延伸,定然有趣的紧,愿抛砖引玉。
- ①老鼠以怎样的策略才能以最短路径成功逃脱?(有限体力)
- ②老鼠以怎样的策略才能以最短时间成功逃脱?(有限氧气)
- ③要想成功逃脱,老鼠的最大速度的最小值是多少?(有限速度)
- ④讨论多只猫或多只老鼠的情形。(策略)
- ⑤讨论不同的水池形状。(边界)
- ⑥讨论在高维空间中的情形。(高维空间)
- ⑦本问题有哪些应用?(应用)
- ⑧问题的起源是什么?(起源)
