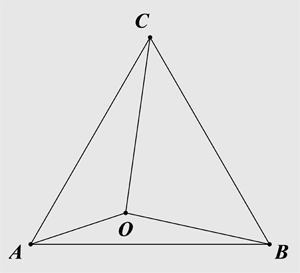
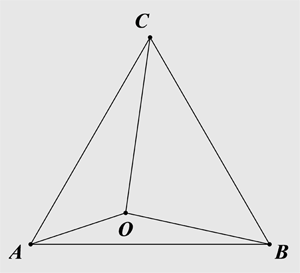
已知：$\Delta ABC$是正三角形，三角形内一点$O$到各顶点$A,B,C$的距离分别是$3,4,5$。求$\Delta ABC$的边长。
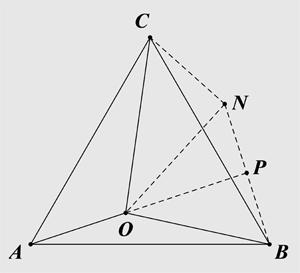
解：作，以$OB$为边作等边$\Delta OBN$，连结$CN$，延长$AO$交$BN$于点$P$。如图所示。
■
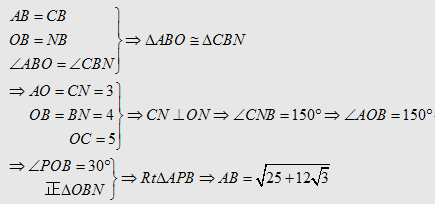
还可以这样做辅助线:
■
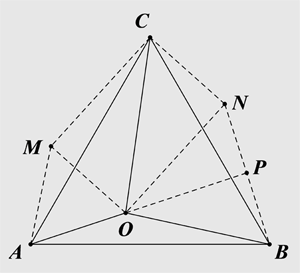
更一般的情况，记 $a=OA,\;b=OB,\;c=OC,\;d=AB$，则有 $3(a^4+b^4+c^4+d^4)=(a^2+b^2+c^2+d^2)^2$。
在初二的时间，父亲见我无事，于是留下此题。不想，这道几何题竟虐了我半年之久。想出方法之后，惊喜若狂（就像《我所理解的数学》中写到的“冥思苦想后的顿悟乃是人间至乐”）。
高中后，喜欢与同学互换经典题目。一次，给一位小学同学CC写信，在最后附上了此题。不久，收到了回信及他的答案，也即本文给出的答案。
后来到了大学，在中学数学竞赛课上，老师又讲到此题，给出的答案中有5条辅助线，由于这几种方法的原理都是一样的，此处不再赘述。
后来想想，此题并不是特别难。关键在于如何利用3，4，5这组勾股数。既然知道它们是勾股数，那么如果把它们放到一个三角形中去，问题基本上就有眉目了。而最容易想到的办法就是把以点为中心顺时针旋转……