
前段时间在博客上发了一篇《双色球是随机的么?》,收到几位朋友的评论,也是本博客为数不多的评论,为了迎合大家的兴趣,故发此篇。
此篇文章的重点还是放在Mathematica这款数学软件在网页数据抓取与定义程序包上,至于双色球嘛,只是个载体。有兴趣的朋友可以将本文中的方法应用到各种你想下载数据的地方,比如:桌面壁纸网站,列表形式的下载地址,网页中指定位置的文本,统计网页中的图片数量或广告位,去掉文字中的干扰码……
关于Mma中的正则表达式和程序包的模板等介绍,请参见《双色球是随机的么?(一)》
1、随机序列
随机序列,即一组随机变量组成的序列。
这个随机变量可以是1维的也可以是多维,通常都是以数字的形式出现(当然也有其它形式,比如:颜色和文字等)。
在生活中随机序列随处可见,例如:拨打n个电话,每个电话的等待时间组成的序列;理想状态下,股票每日的均价组成的序列;赌徒在不出老千的情况下,置出色子的点数组成的序列;当然还有彩票的开奖结果结成的序列。
但是要想检验一个序列是否随机却并不容易,假设一位赌徒连续3次都置出6点,你也不能断定他出了老千。
随机性检验是统计学中一个重要的课题。
就此,Charmaine Kenny 在2005年的一篇报告中给出了一套检验方法—— NIST test suite for random numbers。
主要包含以下子方法:
详见报告
《Random Number Generators: An Evaluation and Compar ison of Random.org and Some Commonly Used Generators》第4.1.5节
○ Frequency Test: Monobit
○ Frequency Test: Block
○ Runs Test
○ Test for the Longest Runs of Ones in a Block
○ Binary Matrix Rank Test
○ Discrete Fourier Transform (Spectral Test)
○ Non-Overlapping Template Matching Test
○ Overlapping Template Matching Test
○ Maurer’s Universal Statistical Test
○ Linear Complexity Test
○ Serial Test
○ Approximate Entropy Test
○ Cumulative Sums Test
○ Random Excursions Test
○ Random Excursions Variant Test
2、红球的随机性检验
在上一篇文章中,用游程检验方法对蓝球的随机性做了检验,此处着重对红球的随机性进行检验,方法呢还是用游程检验。但由于红球是非独立的6维随机变量,没有现成的方法可以对其随机性进行直接检验。笔者首先想到的方法就是将每组红球对应到一个数字,然后根据这一数字的大小或奇偶进行游程检验。
由于红球共有$C_{33}^{6}=1107568$种不同的组合,因此,找到一种双射,使得每组红球都可以对应到1-1107568中的一个数字,那么就可以用流程检验了。下面给出一种满足条件的映射:
首先,将红球按升序排列,并在第1个球之前放置一个占位球,令其号码是0;
记作:$red=\left\{ {{r}_{0}}\ ,\ {{r}_{1}}\ ,\ {{r}_{2}}\ , \cdots\ ,\ {{r}_{6}} \right\}$,其中${{r}_{0}}=0$,${{r}_{1}}<{{r}_{2}}<\cdots <{{r}_{6}}$ ;
然后,写出每个球与前一个球之间的所有数字;
记作:$b=\left\{ \{1,2,\cdots ,{{r}_{1}}-1\},\left\{ {{r}_{1}}+1,\cdots ,{{r}_{2}}-1 \right\},\cdots ,\left\{ {{r}_{5}}+1,\cdots ,{{r}_{6}}-1 \right\} \right\}$
最后,将$b$中的每个元素按以下方式计算,之后求和再加1即可。记${{b}_{ij}}$为$b$中第$i$个表中第$j$个元素,${{n}_{i}}$是$b$中第$i$个表的元素个数,\[S=1+\sum\limits_{i=1}^{6}{\sum\limits_{j=1}^{{{n}_{i}}}{C_{33-{{b}_{ij}}}^{6-i}}}\]
本文中的程序包中只定义了一个函数,而在Mma中的一个程序包中是可以定义多个函数的,使其成为具有某一完整功能程序包,再加上交互式设计就可以开发成一个个工具包了,就想Matlab一样。其实,我一个伟大的梦想,就是能与志同道合的朋友们一起编写Mathematica工具包,使其拓展性和易用性与Matlab一样强大。相应的Mathematica程序包(点此下载)代码如下:
BeginPackage["SCQ`"]
RedToOne::usage = "RedToOne[{r1,r2,r3,r4,r5,r6}] 返回这组红球所对应的数值(1~1107568)。";
Begin["Private`"]
RedToOne=Function[da,
lsda=da;
PrependTo[lsda,0];
nda=Table[Range[lsda[[k]]+1,lsda[[k+1]]-1],{k,1,6}];
count=Table[Sum[Binomial[33-nda[[k,i]],6-k],{i,1,Length[nda[[k]]]}],{k,1,6}];
Total[count]+1];
End[]
EndPackage[]
下面仍然使用上一篇文章中的游检验程序包“Runs.m”,和双色球数据“2003-2013年双色球开奖号码”作随机性检验。检验代码如下:

da = Import["E:\\4Mahtematics\\其它\\双色球\\双色球2003-2013.xlsx"][[1]];
<< "D:/myf/mySCQ.m"
<< "D:/myf/Runs.m"
y = 2013;(*需要检验的年份*)
y = 1000 y;
mda = Select[da, y < #[[1]] < y + 155 &][[;; , 2 ;; 7]] //
Floor;(*从da中提取需要检验的年份*)
pd = Binomial[33, 6]/2 + 0.5;(*计算分界值*)
RedToOne /@ mda;(*RedToOne是调用的上文中介绍的程序包中的函数*)
dx = If[# > pd, 1, 0] & /@ %;(*大小号:大于分界值的记为1,小于的记为0*)
ds = If[EvenQ[#], 0, 1] & /@ %%;(*单双号:双号记为0,单号记为1*)
RunsTest[dx, 0.05](*大小号游程检验*)
RunsTest[ds, 0.05](*单双号游程检验*)
此外,还可以用建立好的双射结果绘制2维或3维散点图,以便直观判断。
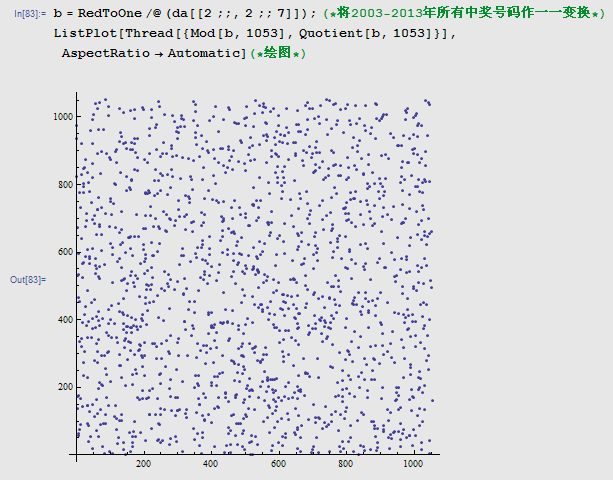
从图型上看,给人的第一感觉:杂乱无章。好,这就是随机性的最大体现!对于其它的检验方法,有兴趣的朋友可以自己试着玩儿一下。
3、抓取中奖分布数据
这里给大家介绍一下Mathematica中“流”的使用方法,实际上它是对文件的底层操作。一般来说,Mma中的流主要是用来读取或存储外部较大文件的,以实现边读边分析或边计算边导出的目的。比如,你电脑内存只有1G,那么是无法将一个2G的文件导入的内存的(虚拟内存除外),这时“流”就派上用场了。而当今是大数据时代,用软盘存储数据的时代已经可以归到考古界了 ^_^ 。
如果网易直接给我们它数据库的地址和具有读权限的用户的话,那用Mma玩起来就更爽了。当然,网易是不会给我们这些的。因此,我们就得自己动手了,简单学一下Mma,写上十来行代码,就可以得到所有你想要的东西。另外,你千万不要搞得太猛,否则被屏蔽IP可就不好玩了。

实际上,用Mma抓取网络数据,完全可以不用“流”就可以轻松搞定。但这里为了展示一下Mma的强大,还是用了一下下。为了不至于茫然地等待,这里还加了进度条和预计的等待时间。Mma代码如下:
下载上面的代码:百度网盘
点此下载导出的中奖分布Excel文件(2012111-2014047-中奖分布.xlsx)>>
点此下载销售量数据的Excel文件(2012111-2012154-销量.xlsx)>>
销售量数据的抓取程序请大家自己试着编一下吧,与上面的代码类似。细心的朋友会还发现销量有个很规律的模式:1高2低循环。再进一步,每周日的销量要比其它两次开奖的销售量要高。此外,从销量还可以看出彩票也有热季和淡季之分!3月和11月前后销量较高,而1月前后和6月则为淡季。
4、中奖分布检验
用卡方拟合检验法检验中奖分布是否符合理论分布 。在Mma中,有很多检验给定数据是否服从指定分布的检验函数(比如:DistributionFitTest、PearsonChiSquareTest、KolmogorovSmirnovTest等),其中指定的分布还可以是自定义的(函数:ProbabilityDistribution)。但由于本例中的数据量太大,所以我们还是用笨方法——从理论出发。
卡方拟合检验的一些合用条件:①样本量在50以上为宜(本例显然满足);②期望数一般不小于5(本例虽然满足,但如果把一等奖和二等奖合并一下会更好些,下面就是用了合并之后的数据进行分析的)。
计算卡方统计量的表达式如下:
\[{{\chi }^{2}}=\sum\limits_{i=1}^{k}{\frac{{{\left( {{f}_{i}}-n{{p}_{i}} \right)}^{2}}}{n{{p}_{i}}}}=\sum\limits_{i=1}^{k}{\frac{{{f}_{i}}^{2}}{n{{p}_{i}}}}-n\]
其中$n$是数据总量,$k$是总组数,${{f}_{i}}$是观测频数,${{p}_{i}}$是对应的假定概率(即${{H}_{0}}$成立时每组的概率),则$n{{p}_{i}}$就是${{H}_{0}}$成立时第$i$组的期望频数。一般要求$n\ge 50$,$\min n{{p}_{i}}\ge 5$,那么当${{H}_{0}}$成立时,可以认为${{\chi }^{2}}$服从自由度为$k-1$的卡方分布。对于本例来说,这些条件全都满足。Mma代码如下:

SetDirectory["E:/4Mahtematics/其它/双色球/双色球奖金/"];(*设置当前目录*)
da1 = Import["2012111-2014047-中奖分布.xlsx"][[1]];(*导入数据*)
da2 = Import["2012111-2012154-销量.xlsx"][[1]];(*导入数据*)
vda = Flatten[#][[{1, 3, 7, 11, 15, 19, 23}]] & /@
Partition[da1, 6];(*整合数据:期,一等奖,二等奖,,六等奖*)
fda = Join[Transpose[vda], {da2[[;; , 2]]}] //
Transpose;(*将销量追加到尾部*)
nfda = Flatten[{#[[1]], #[[2]] + #[[3]], #[[4]], #[[5]], #[[6]], \
#[[7]], #[[8]] - Total[#[[2 ;; 7]]]}] & /@ fda;(*合并一等奖和二等奖*)
p = {16, 162, 7695, 137475, 1043640, 16532100}/Binomial[33, 6]/
16;(*H0成立时的分布列*)
kk = Table[
Total[nfda[[n, 2 ;; -1]]^2/(fda[[n, -1]] p)] - fda[[n, -1]], {n, 1,
Length[fda]}];(*计算卡方统计量*)
Export["D:/卡方统计量.xlsx", {Join[{fda[[;; , 1]]}, {kk}] //
Transpose}];(*导出数据*)
点此下载导出的卡方统计量(2012111-2014047-中奖分布的卡方值.xlsx)>>
从结果可见,2012111期至2014047没有任何一期的中奖分布服从理论分布!乍一看,这确是一个让人吃惊的结果。但这并不能说明彩票有问题,因为,几乎所有的彩民都是分析了前几期的开奖结果才购买的,何况还有大量的合买也会造成一定的影响。另外,这些彩民都是正常的人类,分析逻辑无外乎那么几种。因此,即便我没有彩民选号的数据,但也可以断定彩民购买的号码肯定不是随机的,某些号码被宠爱有些号码被冷落!!这是造成中奖分布不符合理论分布的主要原因。
5、总结
彩民总是关心彩票是否随机,怎样选号才能中奖等等。但是彩民却往往忽略了彩票的本质——募集善款。我想,在我国通过彩票筹集的资金远比慈善机构筹集的要多吧。我们还应该意识到,与发达国家相比,我们的慈善事业还有很长的路要走。
另外,彩迷往往是风险规避者,一般不适合创业!在这篇文章中有些例子不错,正好反应了这一点——《过度自信是创业者的通行证》,大家可以看看。但迷迷们却默默地支持着我国的慈善事业,着实可学可敬。
最后,真心地希望各种彩票都能把另50%的销售额的去向明细公开化,以便让彩民们知道,他们为哪些慈善事业作了贡献。以激励彩民理性购彩,更深刻地认识彩票,至少应该有这样的心态:不中奖是自己为慈善事业作的贡献多些,中奖了是上苍对自己长期作慈善事业的激励与奖励。
