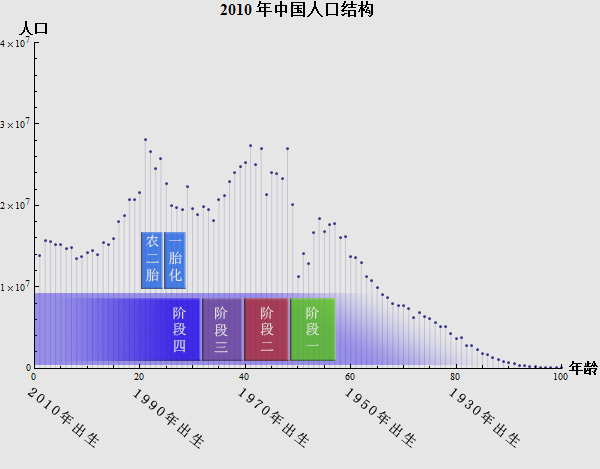
计划生育在我国有着‘悠久’的历史，从1953年提出到1962年实施，从1971年全面开展到1979年的新阶段。每个阶段都有不同的特色。下图是我首发在人大经济论坛上的一份关于我国人口结构的与计划生育的简图，详情请点击本句中的链接查看：

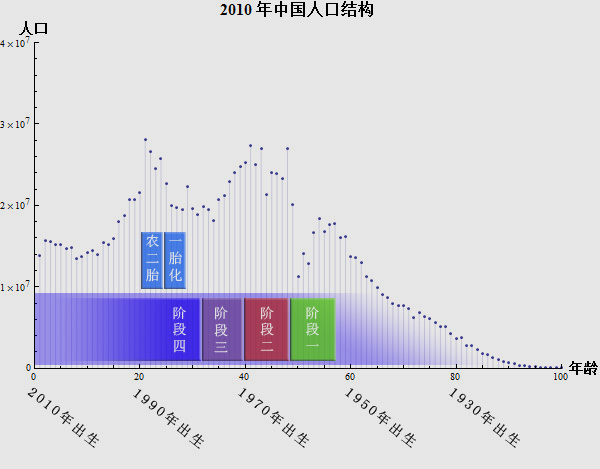
1985年后，农村开始实施二胎化计划生育办法。很多地方都是这样规定的：如果第一胎是男孩，则不可以再生第二胎；但如果第一胎是女孩，则可以再生第二胎，且第二胎不论男女都不允许生第三胎；

乍一看上去容易让人产生错觉：这样的政策会使男性比例增加。但，实则不然，定这样一种政策是经过深思熟虑的，而且非常“美妙”！它不但不会影响男女比例，还给第一胎是女孩的家庭一个生男孩的机会。这让农村中普遍存在的“香火”思想得以放宽，至少会减少“超生游击队”的数量。下面就此产生的一系列相关问题进行讨论。

问题一

如果第一胎是男孩，则不可以再生第二胎；但如果第一胎是女孩，则可以再生第二胎，且第二胎不论男女都不允许生第三胎。问：每个家庭孩子数量的期望是多少？男女比例的理论值是多少？（假定生男生女概率相同且相互独立，下同）

假设每个家庭孩子数量只有两种情况，即1个孩子（男孩），2个孩子（两女，或一女一男），其它情况不考虑在内。

（1）设孩子数量是$X$，则$E\left( X \right)=1\times \frac{1}{2}+2\times \left( \frac{1}{2}\times \frac{1}{2}+\frac{1}{2}\times \frac{1}{2} \right)=\frac{3}{2}$ 。

（2）分别计算每个家庭男孩数量与女孩数量的期望：

\[E\left( {{X}_{M}} \right)=1\times \left( \frac{1}{2}+\frac{1}{2}\times \frac{1}{2} \right)+0\times \left( \frac{1}{2}\times \frac{1}{2} \right)=\frac{3}{4}\]

\[E\left( {{X}_{F}} \right)=1\times \left( \frac{1}{2}\times \frac{1}{2} \right)+2\times \left( \frac{1}{2}\times \frac{1}{2} \right)=\frac{3}{4}\]

由于二者相同，所以男女比例是$1:1$ 。

问题二

政策修改为：直到生下一名男孩才不允许再生，总胎数不限。问题同上。

（1）设$X$代表一个家庭孩子的数量，即第$X$个孩子是个男孩，则有：$P\left( X=n \right)={{\left( \frac{1}{2} \right)}^{n-1}}\frac{1}{2}=\frac{1}{{{2}^{n}}}$

因此，$E\left( X \right)=\sum\limits_{n=1}^{\infty }{nP\left( X=n \right)}=\sum\limits_{n=1}^{\infty }{\frac{n}{{{2}^{n}}}}=2$

（2）

$E\left( {{X}_{M}} \right)=1$

$E\left( {{X}_{F}} \right)=\sum\limits_{n=1}^{\infty }{n\times \frac{1}{{{2}^{n+1}}}}=1$ 或者用这一方法：$E\left( {{X}_{}} \right)=E\left( X \right)-E\left( {{X}_{}} \right)=1$。

所以比例仍是$1:1$ 。

问题三

政策修改为：直到连续出生2个男孩才禁止再生下一胎，总胎数不限。问题同上。

各位朋友可能已经猜到了，男女比例还是$1:1$ 。这是由于，限制条件中仅涉及到了男孩或仅涉及到了女孩，这样的限制条件并不影响生男女的独立性，又由于其概率相同，所以比例还是一样的。对于这一问题不再用概率方法求解，而是改用随机模拟的方式来验证。

很多概率统计问题用严格的理论方法求解是非常困难的，而利用随机模拟的方式却可以很容易去检验。再通过简单的推理，还可以得到相应的置信区间（这里类似于数值计算中的误差），从而可以合理地调节$n$的大小来控制模拟的精度。下面是此问题随机模型的Mathematica程序：

k = n = 100000;
stime = SessionTime[];(*记录开始会话时间*)
ss = Reap[Do[
s = {};
p = RandomInteger[1]; AppendTo[s, p];(*0表示女孩，1表示男孩*)
p = RandomInteger[1]; AppendTo[s, p];(*0表示女孩，1表示男孩*)
While[p == 0 || s[[-2]] == 0,(*判断：本胎是女孩或上一胎是女孩*)
p = RandomInteger[1]; AppendTo[s, p];(*0表示女孩，1表示男孩*)
]
Sow[s]; ctime = SessionTime[];(*记录当前会话时间*)
, {k, 1, n}]];
ss = Flatten[ss[[2]]]; k = n;
Row[{"每个家庭孩子数量的希望为：", ToString[Length[ss]/n // N]}]
Row[{"男孩比例为：", ToString[Total[ss]/Length[ss] // N]}]
Row[{Dynamic["第" <> ToString[k] <> "个家庭。"], ,
ProgressIndicator[Dynamic[k/n]], ,
Dynamic["预计剩余时间：" <>
ToString[NumberForm[N[(n - k) (ctime - stime)/k], {4, 2}]] <>
"秒。"]}]

可见，随机模拟确实奏效，而且问题变得更复杂了之后，随机模拟程序只要稍加改动就OK了，远比重新用概率理论算一便要快。建议，当自己对问题已经有直观判断时，可以先用随机模拟程序测试一下。如果一致，那么基本上你的直观是正确的，继续想下去一般会有理论解法；如果不一致，赶快检验一下哪里想错了，并换个思路考虑问题。

下面这个小问题给特别适合用随机模拟来做，请读者亲自自己尝试一下哪个方法好。

问题：在边长等于1的正方形内随机选2个点，问2点之间距离的期望是多少？

问题四

政策修改为：直到出生的男孩个数比女孩多1个时才禁止再生下一胎，总胎数不限。问题同上。