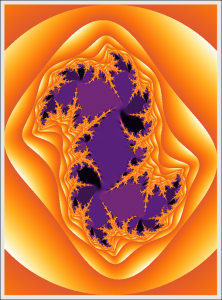
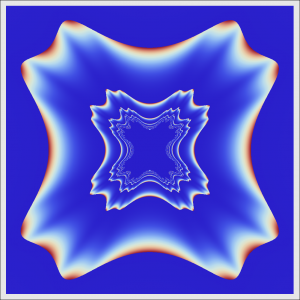
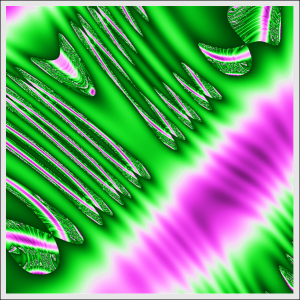
第一篇博文小谈了一下分形。这次再说说分形更灵活的生成方法——无穷迭代。

理论

定义

$F(\mathbf{x} ) \text{:=} \lim_{k\to \infty } f^k(\mathbf{x} )$

其中$\mathbf{x}\in {{\mathbb{R}}^{n}}$，$f\left( \mathbf{x} \right)\in {{\mathbb{R}}^{n}}$，$f\left( \mathbf{x} \right)$定义在$\mathbf{d}$上，值域为$\mathbf{v}$。

${{\mathbf{D}}_{1}}:=\left\{ \mathbf{x}|F\left( \mathbf{x} \right)\ is\ exist\ and\ \left\| F\left( \mathbf{x} \right) \right\|<\infty \right\}$，${{\mathbf{V}}_{1}}:=F\left( {{\mathbf{D}}_{1}} \right)$

${{\mathbf{D}}_{2}}:=\left\{ \mathbf{x}|F\left( \mathbf{x} \right)\ is\ Multi-valued\ and\ \left\| F\left( \mathbf{x} \right) \right\|<\infty \right\}$，${{\mathbf{V}}_{2}}:=F\left( {{\mathbf{D}}_{2}} \right)$

$\mathbf{D}:={{\mathbf{D}}_{1}}\bigcup {{\mathbf{D}}_{2}}$，$\mathbf{V}:=F\left( \mathbf{D} \right)$

容易知道$\mathbf{V}\subset \mathbf{D}$。

如果将$\mathbf{D}$细分，它是由以下点集构成的：①不动点集，②压缩点集，③振荡点集，④^*发散点集。

讨论

当$n=1$时，即便$f\left( \mathbf{x} \right)$是多项式，$\mathbf{D}$和$\mathbf{V}$也是比较复杂的。根据经验$\mathbf{V}$一般是单点集。

当$n=2$时，$\mathbf{D}$和$\mathbf{V}$就更加复杂了，而且还很有趣。为了方便讨论，将上面的定义写成显式的向量形式：\[f{{\left( {{x}_{1}},{{x}_{2}} \right)}^{T}}:={{\left( {{f}_{1}}{{\left( {{x}_{1}},{{x}_{2}} \right)}^{T}},{{f}_{2}}{{\left( {{x}_{1}},{{x}_{2}} \right)}^{T}} \right)}^{T}}\]，其中${{f}_{1}}$和${{f}_{2}}$都是普通的二元函数。当${{f}_{1}}$和${{f}_{2}}$满足柯西－黎曼方程时，这样生成的图形与通过复数生成的分形是一致的。本文中的分形图案主要是由不满足柯西－黎曼方程的${{f}_{1}}$和${{f}_{2}}$生成的，用这样方式生成的分形更加灵活有趣。

当$n=3$时，可以用这种方式生成三维分形。当$n>3$时，可以生成高维分形，但难以表达。

Mathemaitca代码

Fractal2


Remove["Global`*"];
n = 600;(*图像宽度*)
x0 = 10.6; y0 = 10.6;(*绘图范围：{{-x0,x0},{-y0,y0}}*)
st = (2 x0)/n;(*步长*)
ts = 21.5;(*阈值*)
in = 11;(*迭代次数*)
f1 = Function[{x, y}, x^2 - y^2 - Cos[y^2] + 0.285];(*f的第一个分量f1*)
f2 = Function[{x, y}, Sin[x - y] + x - y - 0.3];(*f的第二个分量f2*)
f = Function[xy, {f1[xy[[1]], xy[[2]]], f2[xy[[1]], xy[[2]]]}];(*f*)
da = Table[
Norm[NestWhile[f, {x, y}, Norm[#] < ts &, 1, in]], {y, -y0, y0,
st}, {x, -x0, x0, st}];(*生成分形数据*)
ArrayPlot[da/Max[da], ColorFunction -> "GreenPinkTones",
ImageSize -> (Floor[2 x0/st] + 1)](*绘图*)