几何体表面的最短距离

514 11 2014年7月31日

经典问题

已经有一个月没写博客了，想想，还是偷个懒儿，用几分钟的时间凑一篇吧。

很久之前见过这样一道题：

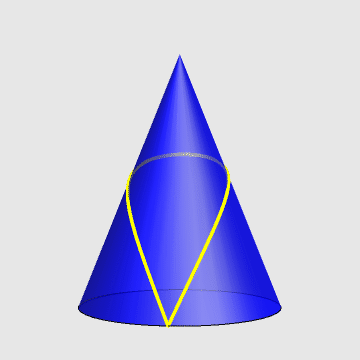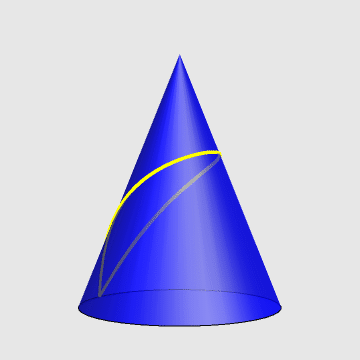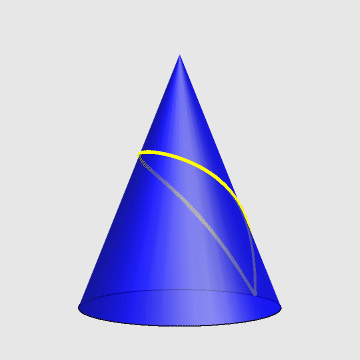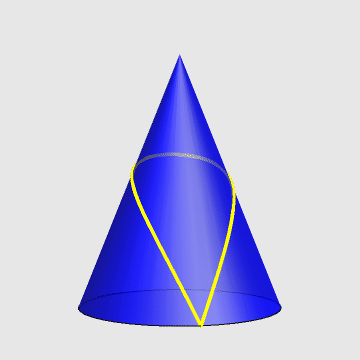
一只蚂蚁，从一圆锥的底边出发，绕圆锥一周又回到起点。求最短路径。

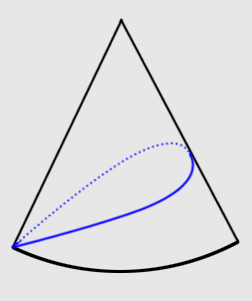
Tapered

衍生题

题目

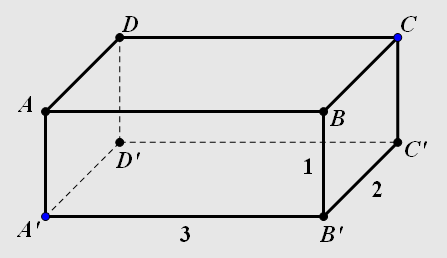
Cuboid
  1. 在长，宽，高分别为 1，2，3 的长方体表面上，蚂蚁想从A’点到对角的C点。求其最短路径。（虽然很相似，但肯定会有人做错）；
  2. 针对原题，假定圆锥高为h，底面半径为r，求蚂蚁的轨迹方程。

参考答案

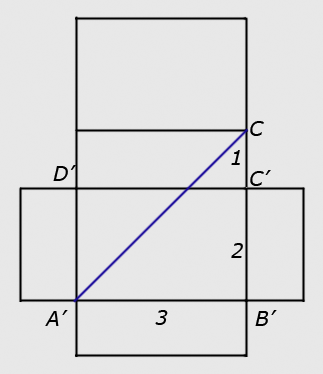
1、答案：$2\sqrt{3}$。

从A’点到C点的简单路径共有6条，长度有3种，分别是 $\sqrt{1+{{\left( 2+3 \right)}^{2}}}$，$\sqrt{2+{{\left( 1+3 \right)}^{2}}}$，$\sqrt{3+{{\left( 1+2 \right)}^{2}}}$。

参考图：

321

2、参数方程如下：

$r$是圆锥半径，$h$圆锥高，记：

$$R=\sqrt{{{h}^{2}}+{{r}^{2}}}$$

$$\alpha =\frac{\cos \frac{r}{R}\pi }{\cos \frac{r}{R}\left( t-\pi \right)}$$

$$\beta =\frac{\cos \frac{r}{R}\pi }{\cos \frac{r}{R}\left( t-\pi \right)}$$

则方程为：

\[\left\{ \begin{align} & x=\alpha r\cos t \\ & y=\alpha r\sin t \\ & z=h\left( 1-\beta \right) \\ \end{align} \right.\]

其中，$t\in \left[ 0,2\pi \right]$

参考图：

mind

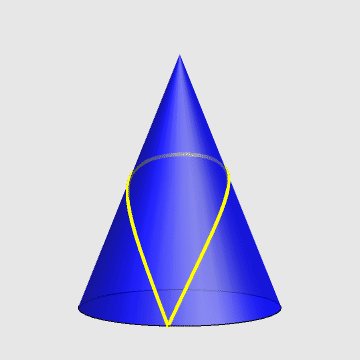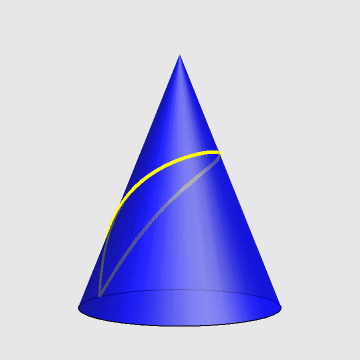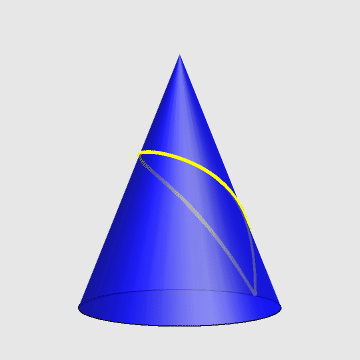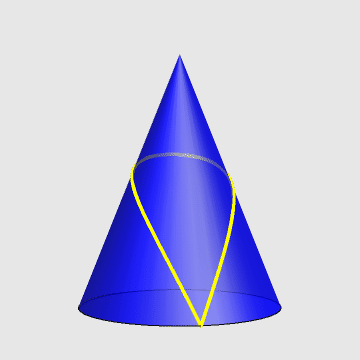
生成上图的代码：

r = 1;
h = 2.5 r;(* h>Sqrt[3]r *)
R = Sqrt[h^2 + r^2];
p1 = Graphics3D[{Blue, Opacity[0.6], Specularity[White, 20], 
    Lighting -> "Neutral", Cone[{{0, 0, 0}, {0, 0, h}}, r]}, 
   Boxed -> False, Background -> GrayLevel[231/255]];(*圆锥面*)

p2 = ParametricPlot3D[{r (Cos[Pi r/R]/Cos[t r /R - Pi r /R]) Cos[t], 
    r (Cos[Pi r/R]/Cos[t r /R - Pi r /R]) Sin[t], 
    h (1 - Cos[Pi r /R]/Cos[(t - Pi) r/R])}, {t, 0, 2 Pi}, 
   Mesh -> None, PlotRange -> {{-r, r}, {-r, r}, {-h/4, 5 h/4}}, 
   PlotStyle -> Directive[Yellow, Thickness[0.01]], Axes -> None, 
   Boxed -> False, BoundaryStyle -> None, 
   Background -> GrayLevel[231/255], MaxRecursion -> 6];(*曲线*)

ps = Table[
   Show[{p1, p2}, SphericalRegion -> True, ViewAngle -> 0.5, 
    ViewVector -> {7 Cos[t], 7 Sin[t], h/2}], {t, 0.1, 2 Pi, 0.2}];

Export["E:/mind.gif", ps]