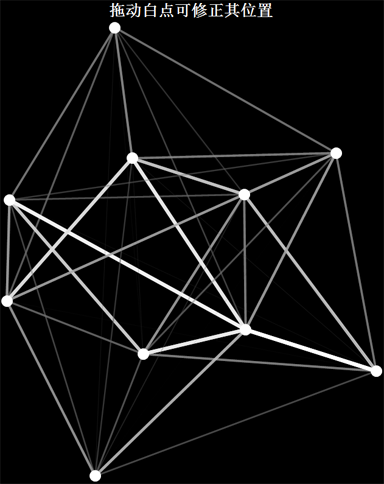
力导向图简介
力导向图的英文名是 Force-Directed Graph,看大家都这么翻译也就这么写了。
问题背景:
现有若干点及其部分或全部边,求每点的位置,使其能够更美观地展现出来。
将边从直线转换为适当的曲线,可以使图更加美观。
与多维尺度方法的目的有些相像。(话说,我很想知道“多维尺度”这个词为什么被墙了呢,还是看英文的吧)
在应用中,通常还有一个相关性的限制条件:两点的相关性越强,相距应该越近。
有时候也会有其它限制条件,比如:边尽可能不相交。
由于要直观简洁,所以一般只在2维或3维空间中作图。
有些问题之所以困难,是由于它有太多的限制条件。
而此问题困难,却是由于其限制条件太少了!
写此文是由于在Mma中没找到相应的函数
在Mma中有很多数据可视化函数,其中社区图函数(CommunityGraphPlot)就是其中一个。但是,它只能展示点与点之间是否有关系,以及哪些点可以构成一个社区,但不能包含关系的强弱信息。
针对这一点,”Force-Directed Graph”(通常被译为”力导向图”)是一个非常有力的工具。
它可以使关系越强的点相距越近,无关或关系越弱的点相距越远。
这就将点之间的关系直观地展现出来了。
基本绘制方法
下面仅介绍比较原始的方法,改进方法请参见附件中的参考文献。
>>下载附件(程序+详细说明+参考文献)
程序虽然没做优化,但还是很好玩的,可以实现人机交互以修改坐标。
大方向:
让任意两点之间都存在斥力,可以使它们不会相距太近
让有关系的点之间存在引力,可以使它们不会相距太远
力学模型:
条件:所有点之间都存在斥力和引力,其中引力根据点之间的相关性和距离而定,斥力仅根据点之间的距离而定。
目标:计算出其中一个稳态(不唯一)。
方法:让它们在空间中自己玩耍,玩累了就停,也就是所要求的稳态。
方法中的”放”、”玩”、”累”都是有讲究的,此处不多说,想了解的看附件或自己查资料。
举个形像的例子:
条件:每个点都带有等量的正电荷,存在关系的两点之间有一根橡皮筋且关系越强橡皮筋的劲度系数越大。
方法:将其随机放在空间中(点与点之间不要相距太远也不要相距太近,也可以使用多维尺度方法先处理一下),让它们根据受力情况自由运动,同时增加适当的阻力以便系统最终能够停下来。
代码与说明
1、维度(cD),点数(cN),相关矩阵(mR)
完全相关:1
完全无关:0
自身之间:0
cN = 10;(*点数,为产生随机模拟数据,故此先赋值,实际中直接导入相关系数矩阵即可*)
mR = UpperTriangularize[RandomReal[1, {cN, cN}], 1];
mR = Rescale[mR + Transpose[mR]];
cD = 2;
cN = Length[mR];
2、位置列表(lP),质量列表(lM),速度列表(lV)
时间步长(cT),阻尼(cR),动能函数(fE),动能(vE),动能阈值(cE),
cT = 0.1;(*使用渐短步长更为合适*)
cR = 0.99;(*为简单起见,计算完所有速度之后,以此系数乘之*)
lP = RandomReal[20, {cN, cD}];
lM = ConstantArray[100, cN];
lV = ConstantArray[0, {cN, cD}];
fE[lV_] := lM.(Total[#^2] & /@ lV)/2;
(*可以定义其它的动能,以提高计算速度*)
cE = 10^-10;
3、距离函数(fDis),距离矩阵函数(fmDis),方向矩阵函数(fDir)
这里使用欧几里得距离。
其它距离也可以,比如绝对值距离,可以加快运行速度。
fDis[x1_, x2_] := EuclideanDistance @@ N[{x1, x2}, 20];
mfDis[lP_] := Outer[fDis, lP, lP, 1];
fDir[x1_, x2_] := Normalize@N[x1 - x2, 20];
mfDir[lP_] := Outer[fDir, lP, lP, 1];
4、引力函数(fAF),斥力函数(fRF),合力矩阵(mF)
k0 = 1;(*力函数中的系数*)
fAF[d_] := d^2/k0;
fRF[d_] := If[d < 10^-10, 0, -k0^2/d];
SetAttributes[{fAF, fRF}, Listable];
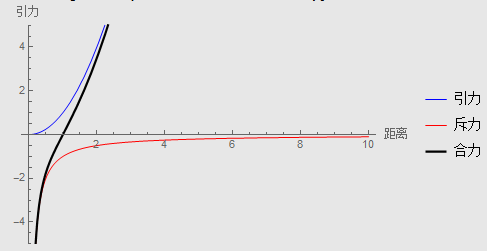
这样定义的力函数,全力如下图所示:
5、距离矩阵(mDis),方向矩阵(mDir),合力(mF),速度(lV),动能(vE)
mDis = mfDis[lP]; mDir = mfDir[lP]; lF = Total[(fAF[mDis] mR + fRF[mDis]) mDir]; lV = (lV + cT lF) cR/lM; vE = fE[lV]; lP = lP + lV;(*更新点坐标*)
再之后循环运行就OK了。
放个测试图
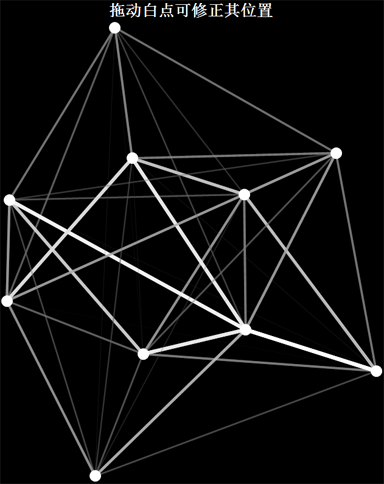
下篇博文预告:《力导向图的应用——明朝那些事儿中的人物关系》,含3维动画的绘制方法哦!
