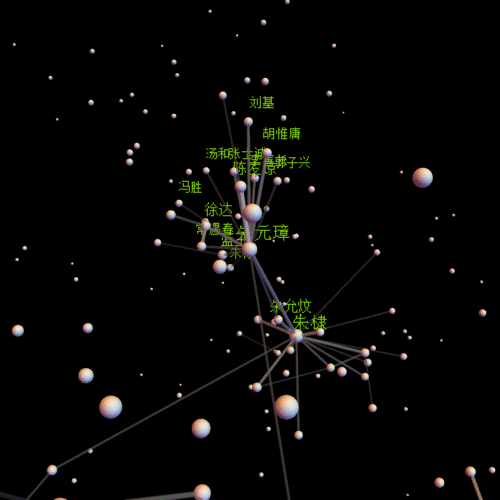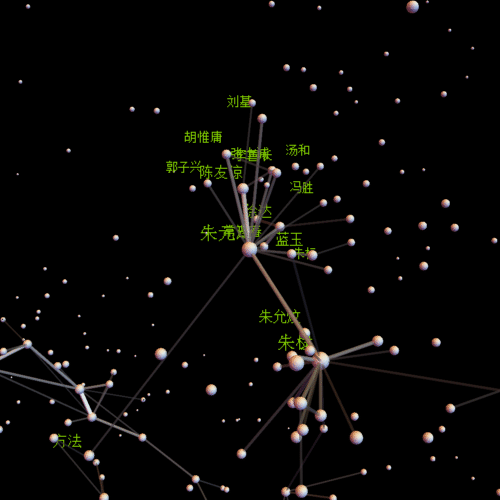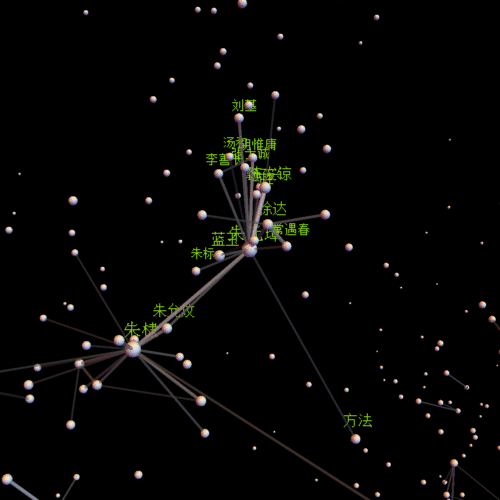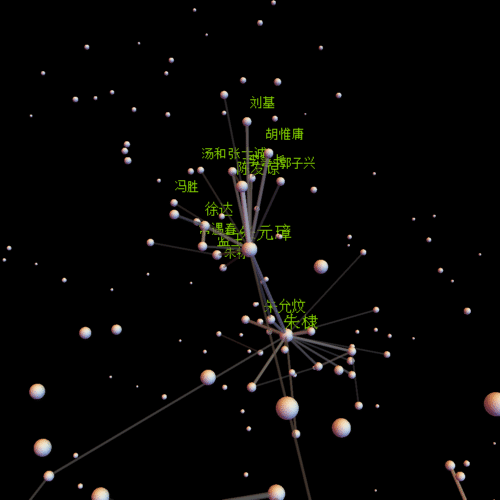
还是先放一张图比较好吧,哈哈
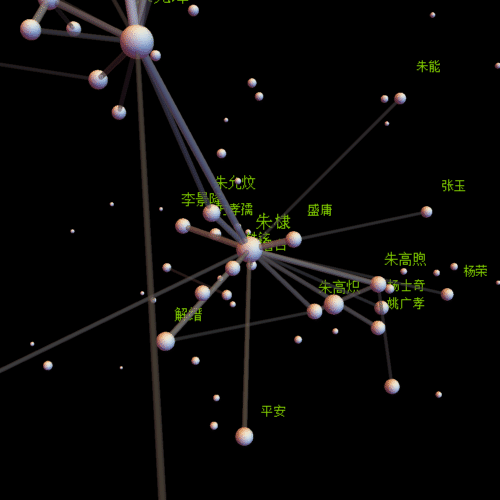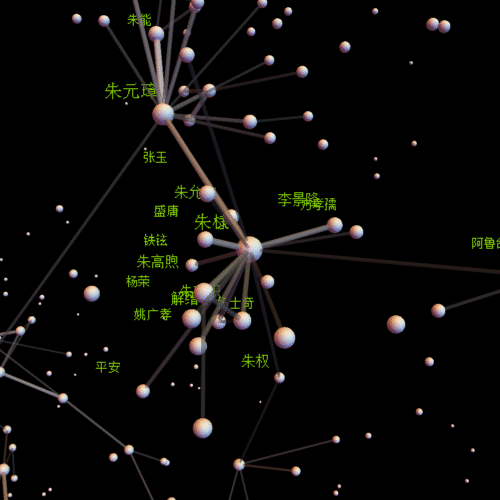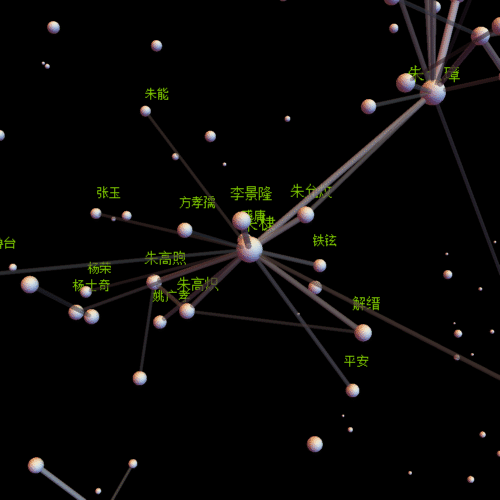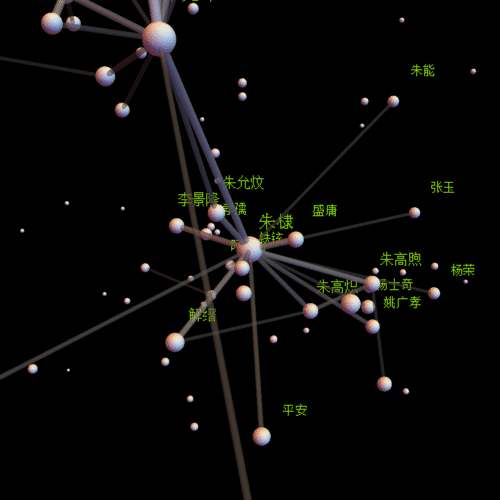
作为上一篇博文的应用篇,很有意思哦,同时又比较繁琐。
为了降低繁琐的工作量,所以需要牺牲一下准确性,在下面的统计分析中仅对文本做了粗略的处理工作。不过,也基本上过得去,不要太计较,我只是为了快乐地玩耍。
常见的问题(有的已经做了处理,有的尚未处理):
● 多人一名(重名)
● 一人多名(多种称呼,自己改过名,身份变更)
● 姓名包含(比如:脱脱,脱脱不花,这是两个人,)
● 语句中包含非人名的人名(比如有这样一句话“一张信用卡”,而有一哥们就叫“张信”)
● 名字起得太语言化(有一个叫“方法”的人)
● 人名中存在Unicode字符集中没有的汉字
● 难以区分的代词或称谓(你,我,他,父亲,太子……)
……
上面只是清洗数据时的麻烦,在调试程序时还会遇到更多的麻烦。比如:
- 582个点运行起来还是挺慢的,因此程序有待优化
- 大于等于3个点时,最终稳态就不唯一了,更别说500多个点了,因此初始状态很重要
- 连线较多时,由于想要以不同的颜色展示,因此黑背景时只能浅色线压深色线
获取数据
为了快速进入玩耍状态,需要去找些数据。主要数据来源的网站都在这儿了:
通用汉字数据:汉语国际教育技术研发中心,中国语言文字网:已经发布的语言文字规范
明朝人物数据:维基百科:明史人物列表,中国历史著名人物
《明朝那些事儿》:Ebook Search Engine(非常给力的电子书搜索引擎,献给有银子买Kindle没银子买电子书的朋友,墙外)
所有数据已经打包在附件中了,下载地址在本文最后。
代码与说明
运行下面代码之前,请先将附件解压至某合适的目录中,目录中尽量不要包含杂七杂八的字符(比如破折号“——”)。
1、统计数据
1.1、 导入数据
path = NotebookDirectory[];
hz = Flatten@
Import[path <> "Data\\汉字列表(增删处理后,共计8275字).xlsx", {"Data",
"数据"}];(*所有简体汉字*)
names = Import[
path <> "Data\\明史人物列表.xlsx", {"Data", "数据", All, {3, 4, 5, 6}}][[
2 ;;]];(*明朝人名单*)
names = Select[#, StringLength[#] > 0 &] & /@ names;(*明朝人名单*)
name = names[[;; , 1]];(*明朝人名单,主名*)
cc = Select[names, Length[#] > 1 &];(*有别名的人名单*)
cc = Thread[# -> #[[1]]][[2 ;;]] & /@ cc;(*替换规则*)
1.2、导入书籍并清洗
book = Import[path <> "Data\\明朝那些事儿\\明朝那些事儿*.txt"];(*导入书籍*)
book = StringJoin[book];(*将7本书合并*)
book = StringReplace[book, "\n" .. -> "\n"];(*去掉重复的换行*)
book = StringReplace[book,
Except[{"\n", ",", "。", "!", "?"}~Join~hz] .. ->
""];(*除汉字和常用标点外,全部删除*)
sentences =
Select[StringSplit[book, "\n"],
StringLength[#] > 1 &];(*按段落拆分文章,并过滤掉长度小于2的段落*)
sentence = StringReplace[#, Flatten[cc]] & /@ sentences;(*替换别名为首列名称*)
name = Pick[name, StringContainsQ[ls, #] & /@ name, True];(*书中出现过的名字*)
1.3、统计数据&保存备用
comNames =
Select[Union[StringCases[#, name]] & /@ sentence,
Length[#] > 1 &];(*出现在同一段落的名字并去重,忽略只有一个人名的段落*)
comName = Union[Flatten[comNames]];(*有哪些名字出现过,忽略只有一个人名的段落*)
ls = StringJoin[sentence];
comNameN = StringCount[ls, #] & /@ comName;(*名字出现的次数*)
coxM = Association @@
Flatten[{#[[1]] -> #[[2]], RotateLeft[#[[1]]] -> #[[2]]} & /@
Tally[Sort /@
Flatten[Subsets[#, {2}] & /@ comNames,
1]]];(*相关度-出现在同一段落名字的次数统计*)
n0 = Length[comName];
mR = Table[ls = coxM[{comName[[m]], comName[[n]]}];
If[Head[ls] == Integer, ls, 0, 0], {m, n0}, {n, n0}];(*相关矩阵*)
Save[path <> "Data/Data", {mR, comName, comNameN}](*保存数据*)
1.4、人名频数概况
- >>统计数据下载(人名频数概况)
- 出现最多的名字(前20)
| 名字 | 出现次数 (忽略一个段落中只含一个名字) |
| 朱棣 | 1425 |
| 朱元璋 | 1419 |
| 徐阶 | 744 |
| 张居正 | 634 |
| 严嵩 | 597 |
| 王守仁 | 534 |
| 袁崇焕 | 531 |
| 朱祁镇 | 448 |
| 魏忠贤 | 448 |
| 胡宗宪 | 406 |
| 也先 | 384 |
| 高拱 | 377 |
| 朱厚照 | 339 |
| 陈友 | 330 |
| 陈友谅 | 328 |
| 戚继光 | 311 |
| 夏言 | 299 |
| 于谦 | 288 |
| 李如松 | 283 |
| 方法 | 274 |
- 出现最多的结合(前20)
| 名字1 | 名字2 | 同段出现次数 |
| 严嵩 | 徐阶 | 149 |
| 朱元璋 | 陈友谅 | 93 |
| 高拱 | 张居正 | 90 |
| 也先 | 朱祁镇 | 71 |
| 徐阶 | 高拱 | 66 |
| 朱棣 | 朱元璋 | 61 |
| 严嵩 | 夏言 | 60 |
| 汪直 | 胡宗宪 | 60 |
| 朱棣 | 盛庸 | 58 |
| 徐阶 | 严世蕃 | 53 |
| 徐达 | 常遇春 | 52 |
| 徐阶 | 张居正 | 52 |
| 朱棣 | 李景隆 | 50 |
| 朱元璋 | 胡惟庸 | 50 |
| 毛文龙 | 袁崇焕 | 50 |
| 朱棣 | 朱允炆 | 48 |
| 朱棣 | 朱高煦 | 45 |
| 朱棣 | 解缙 | 43 |
| 徐达 | 朱元璋 | 41 |
| 朱祁钰 | 朱祁镇 | 41 |
1.5、单词云图
出现次数大于10次的名字,共计255个,忽略只有一个人名的段落。
Remove["Global`*"];
path = NotebookDirectory[];
<< (path <> "Data/Data");(*导入数据*)
<< (path <> "pic2D/PData51727");(*导入数据*)
p = Flatten[Position[comNameN, _?(# > 10 &)]];
name = comName[[p]];
nameN = comNameN[[p]];
n = Length[name];
img = WordCloud[nameN -> name, Background -> GrayLevel[231/255],
ImageSize -> {650, 650}, FontFamily -> "微软雅黑", MaxItems -> n,
WordOrientation -> "Random"]

2、绘制2维力导向图
2.1、计算所需数据
在看长长的程序之前,先看一张运行时的动态图吧,也许能增加你的兴趣。一共迭代了1727次,压缩成87帧的动画,其中有两次手动调整(画面有跳跃的时候,实际上第一帧的时候就有手动调整)。

(*--------------------------导入数据------------------------*)
Remove["Global`*"];
path = NotebookDirectory[];
<< (path <> "Data/Data");(*导入数据,注意路径*)
mR = Rescale[N[mR, 20]];(*将相关矩阵的取值调整到0~1*)
comNameN = Rescale[N[comNameN, 20]];(*将人名出现次数列表的取值调整到0~1*)
(*-----------------------初始化数据---------------------------*)
cD = 2;(*维数,注意修改为3时,需要修改lP定义,以及绘图函数*)
cE = 0.1;(*停止动能阈值*)
cT = 0.5;(*使用渐短步长更为合适*)
cR = 0.99;(*为简单起见,计算完所有速度之后,以此系数乘之*)
cN = Length[comName];(*人名数量*)
lM = 100 comNameN + 10;(*用人名出现次数构造质量列表*)
lV = ConstantArray[0, {cN, cD}];(*初始速度*)
fE[lV_] := lM.(Total[#^2] & /@ lV)/2;(*可以定义其它的动能,以提高计算速度*)
fDis[x1_, x2_] := EuclideanDistance @@ N[{x1, x2}, 20];(*距离函数*)
mfDis[lP_] := Outer[fDis, lP, lP, 1];(*距离矩阵函数*)
fDir[x1_, x2_] := Normalize@N[x1 - x2, 20];(*方向函数*)
mfDir[lP_] := Outer[fDir, lP, lP, 1];(*方向矩阵函数*)
k0 = 1;
fAF[d_] := If[d > 10^10, 100, d^2/k0](*引力函数*)
fRF[d_] := If[d < 10^-10, 0, -k0^2/d];(*斥力函数*)
SetAttributes[{fAF, fRF}, Listable];(*设置函数具有列表属性*)
SeedRandom[2015];(*随机种子*)
ww = RandomPrime[{cN + 1, 10^10}];(*随机相位*)
lP = N[Table[
3/(comNameN[[k]] + 0.25) k0 {Cos[2 Pi ww k/cN],
Sin[2 Pi ww k/cN]}, {k, cN}], 20];(*各点的初始位置*)
(*------------------------计算与保存数据--------------------------*)
Dynamic[Column[{vE,k,Graphics[Flatten[{Table[{Thickness[0.005lineV[[\
k]]],GrayLevel[lineV[[k]]+0.01],Line[{lP[[line[[k,1]]]],lP[[line[[k,2]\
]]]}]},{k,Length[line]}],Table[{GrayLevel[comNameN[[k]]^(1/5)],\
PointSize[0.01comNameN[[k]]^(1/5)],Point[lP[[k]]]},{k,Length[comNameN]\
}]}],Background\[Rule]Black,ImageSize\[Rule]Large,Frame\[Rule]True]}]]\
(*动态显示当前动能及各点位置,会降低运行速度,建议流离注释掉*)
Dynamic[Column[{vE, k}]](*实时却能与迭代次数*)
vE = cE + 100.;(*动能初值*)
k = 0;(*迭代次数初值*)
While[vE > cE,
Parallelize[k += 1;
Save[path <> "pic" <> ToString[cD] <> "D/PData" <> ToString[k],
lP];(*保存数据*)
Export[path <> "pic" <> ToString[cD] <> "D/img" <> ToString[k] <>
".png", Graphics[
Flatten[{Table[{Thickness[0.005 lineV[[k]]],
GrayLevel[lineV[[k]] + 0.01],
Line[{lP[[line[[k, 1]]]], lP[[line[[k, 2]]]]}]}, {k,
Length[line]}],
Table[{GrayLevel[comNameN[[k]]^(1/5)],
PointSize[0.01 comNameN[[k]]^(1/5)], Point[lP[[k]]]}, {k,
Length[comNameN]}]}], Background -> Black,
ImageSize -> {500, 500}]];(*保存图片*)
mDis = mfDis[lP];(*计算距离矩阵*)
mDir = mfDir[lP];(*计算方向矩阵*)
lF = Total[(fAF[mDis] mR + fRF[mDis]) mDir];(*计算合力列表*)
lV = (lV + cT lF) cR/lM;(*计算速度列表*)
vE = fE[lV cT];(*计算此当前动能*)
lP = lP + lV cT;(*更新各点位置*)
]]
(*------------------------手动调整--------------------------*)
(*可以边运行边调整,也可以先停止计算再调整(但在恢复计算时需要修改迭代次数k)*)
LocatorPane[Dynamic[lP],Dynamic[Column[{vE,Graphics[Flatten[{Table[{\
Thickness[0.005lineV[[k]]],GrayLevel[lineV[[k]]+0.01],Line[{lP[[line[[\
k,1]]]],lP[[line[[k,2]]]]}]},{k,Length[line]}],Table[{GrayLevel[\
comNameN[[k]]^(1/5)],PointSize[0.01comNameN[[k]]^(1/5)],Point[lP[[k]]]\
},{k,Length[comNameN]}]}],Background\[Rule]Black,ImageSize\[Rule]{\
1500,1500}]}]],Appearance\[Rule]None](*手动调整点的位置,会降低运行速度,建议流离注释掉*)
2.2、绘图
Remove["Global`*"];
path = NotebookDirectory[];
<< (path <> "Data/Data");(*导入数据*)
<< (path <> "pic2D/PData1727");(*导入数据*)
mR = Rescale[N[mR, 20]];(*将相关矩阵的取值调整到0~1*)
comNameN = Rescale[N[comNameN, 20]];(*将人名出现次数列表的取值调整到0~1*)
line = Position[UpperTriangularize[mR], _?Positive];(*有关系的点对*)
lineV = mR[[Sequence @@ #]] & /@ line;(*对应值*)
line = line[[Ordering[lineV]]];(*有关系的点对,按对应值排序,保证关系强的线在弱线的上面*)
lineV = lineV[[Ordering[lineV]]];(*对应值,按对应值排序*)
img = Graphics[Flatten[{
Table[{Thickness[0.005 lineV[[k]]^(1/2)],
GrayLevel[lineV[[k]] + 0.01],
Line[{lP[[line[[k, 1]]]], lP[[line[[k, 2]]]]}]}, {k,
Length[line]}](*线*),
Table[{GrayLevel[comNameN[[k]]^(1/5)],
PointSize[0.01 comNameN[[k]]^(1/5)], Point[lP[[k]]]}, {k,
Length[comNameN]}](*点*),
Table[
Inset[Style[comName[[k]], FontFamily -> "微软雅黑",
12 comNameN[[k]]^(1/5) + 6, RGBColor[0.5, 0.8, 0]],
lP[[k]] + 0.4 comNameN[[k]]^(1/5)], {k,
Length[comNameN]}](*标注人名*)}]
, Background -> Black, ImageSize -> {4000, 4000},
PlotRange -> {{-30, 30}, {-30, 30}}];(*绘局部图*)
If[FileNames[path <> "pic2D"] == 0,
CreateDirectory[path <> "pic2D"]];(*如果没有目录则自动创建*)
Export[path <> "pic2D/img.png", img];(*导出图像*)
3、绘制3维力导向图
如果不将3维图像做成动画,那么和2维也没什么分别。数据的计算2维图数据计算差不多,只需要把cD赋值为3,lP的初始位置需要修改,最后画图需要修改,其它都是一样的。
各点的初始位置
lP = N[Table[
3/(comNameN[[k]] +
0.25) k0 {Cos[2 Pi ww k/(Floor[Sqrt[cN] + 1])] Cos[
Pi k/(Floor[Sqrt[cN] + 1])] + RandomReal[0.2],
Sin[2 Pi ww k/(Floor[Sqrt[cN] + 1])] Cos[
Pi k/(Floor[Sqrt[cN] + 1])] + RandomReal[0.2],
Sin[ Pi k/(Floor[Sqrt[cN] + 1])]}, {k, cN}], 20];(*各点的初始位置*)
绘图与导出动画
Remove["Global`*"];
path = NotebookDirectory[];
<< (path <> "Data/Data");(*导入数据,注意路径*)
<< (path <> "pic3D/PData1243");(*导入数据,注意路径*)
mR = Rescale[N[mR, 20]];(*将相关矩阵的取值调整到0~1*)
comNameN = Rescale[N[comNameN, 20]];(*将人名出现次数列表的取值调整到0~1*)
st = 2 Pi/60;(*60:动画帖数*)
line = Position[UpperTriangularize[mR], _?(# > 0.1 &)];(*相关系数大于0.1的点对*)
lineV = mR[[Sequence @@ #]] & /@ line;(*对应值*)
line = line[[Ordering[lineV]]];(*有关系的点对,按对应值排序,保证关系强的线在弱线的上面*)
lineV = lineV[[Ordering[lineV]]];(*对应值,按对应值排序*)
centername = "朱元璋"; center =
Position[comName, centername][[1, 1]];(*视点中心*)
insetP = Intersection[Flatten[Position[comNameN, _?(# > 0.01 &)]],
Flatten[Select[line, #[[1]] == center || #[[2]] == center &]] //
Union];(*需要标注姓名的点*)
pics = With[{obj = Graphics3D[Flatten[{
Table[{Opacity[lineV[[k]]^(1/2)], GrayLevel[lineV[[k]]^(1/2)],
Cylinder[{lP[[line[[k, 1]]]], lP[[line[[k, 2]]]]},
0.2 lineV[[k]]^(1/2)]}, {k, Length[line]}](*线*),
Opacity[1],
Table[{GrayLevel[0.9],
Sphere[lP[[k]], 0.5 comNameN[[k]]^(1/5)]}, {k,
Length[comNameN]}](*点和人名*),
Table[
Inset[Style[comName[[insetP[[k]]]], FontFamily -> "宋体",
12 comNameN[[insetP[[k]]]]^(1/5) + 6,
RGBColor[0.5, 0.8, 0]], lP[[insetP[[k]]]] + 1], {k,
Length[insetP]}](*标注姓名*)}]
, Background -> Black, Boxed -> False, ImageSize -> {500, 500}]},
Table[Show[obj, SphericalRegion -> True,
ViewVector -> {{30 Cos[t], 30 Sin[t], 0} + lP[[center]],
lP[[center]]}], {t, st, 2 Pi,
st}]];(*生成动画的每一帖,通过参数ViewVector可以自定义观察轨迹*)
If[FileNames[path <> "pic3D"] == 0,
CreateDirectory[path <> "pic3D"]];(*如果没有目录则自动创建*)
Export[path <> "pic3D/imgs.gif", pics];(*导出动画*)
全图

朱元璋
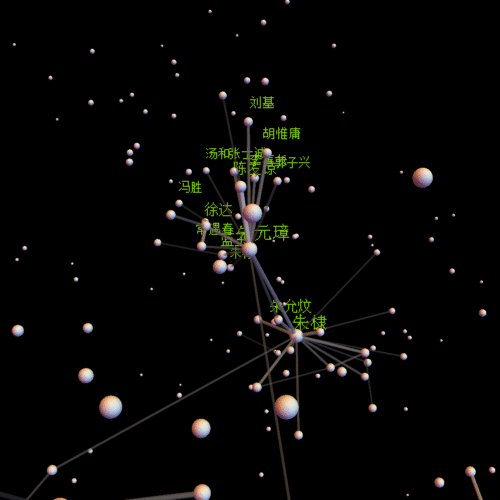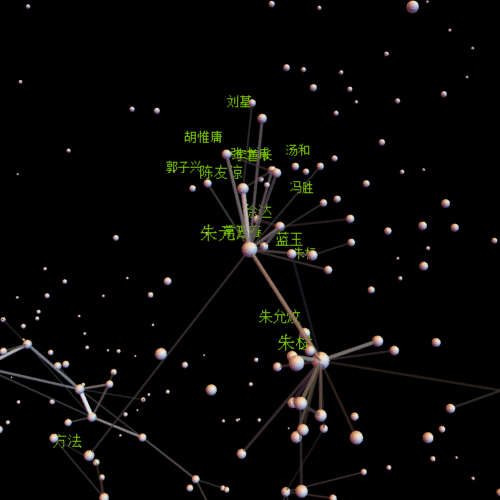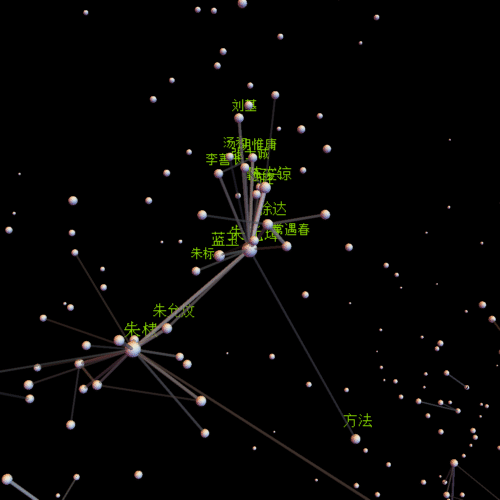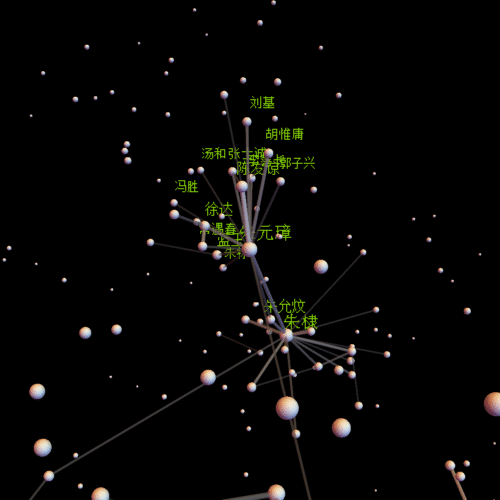
朱棣


