最近有一同学，问起主成分分析（非统计专业也要主元分析）的相关问题，正好我也把知识整理一下。话说主成分分析和因子分析不分家，那么再整理的话，下篇就是《[笔记]因子分析》了。

1、理论

设有$n$个样品，每个样品有$p$个指标。通常这$p$个指标存在一定的关系，因此用更少的综合性指标作为新指标来描述样品，这样更利于分析数据。

为了简单起见，用原指标的线性组合生成新指标。同时还要求第一个新指标的方差最大，第二个新指标的方差次之，而且还与第一个新指标不相关，第三个新指标再次之，而且与前两个新指标都不相关，依次类推，直至找出所有线性无关的新指标。因此新指标的个数应该是原指标的秩。

1.1、从协方差矩阵出发

记${{x}_{i}}$是第$i$个指标的随机变量，$\underset{p\times 1}{\mathop{x}}\,={{\left( {{x}_{1}},{{x}_{2}},\cdots ,{{x}_{p}} \right)}^{T}}$是$p$维随机向量，$\underset{p\times p}{\mathop{\mathbf{V}}}\,=\left( \operatorname{cov}\left( {{x}_{i}},{{x}_{j}} \right) \right)$是$x$的协方差矩阵。

现想要求得一个单位向量$\underset{p\times 1}{\mathop{a}}\,={{\left( {{a}_{1}},{{a}_{2}},\cdots ,{{a}_{p}} \right)}^{T}}$使得，$\underset{1\times 1}{\mathop{y}}\,={{a}^{T}}x$方差最大。

即条件极值问题：

\[\underset{\left| a \right|=1}{\mathop{\max }}\,D\left( {{a}^{T}}\mathbf{X} \right)=\underset{\left| a \right|=1}{\mathop{\max }}\,{{a}^{T}}\mathbf{V}a=\underset{\left| a \right|=1}{\mathop{\max }}\,\frac{{{a}^{T}}\mathbf{V}a}{{{a}^{T}}a}={{\lambda }_{\max }}\]

这里${{\lambda }_{\max }}$是$\mathbf{V}$的最大特征值，此时$a$是对应的特征向量（单位化）。

取向量$\underset{p\times 1}{\mathop{{{a}_{i}}}}\,$为$\mathbf{V}$的第$i$个特征值对应的特征向量（单位化），则有$D\left( {{y}_{i}} \right)=D\left( a_{i}^{T}x \right)={{\lambda }_{i}}$，且$\operatorname{cov}\left( {{y}_{i}},{{y}_{j}} \right)={{\delta }_{ij}}{{\lambda }_{i}}$。这正是我们想要的$\underset{p\times r}{\mathop{\mathbf{A}}}\,=\left( {{a}_{1}},{{a}_{2}},\cdots ,{{a}_{r}} \right)=:{{\left( {{a}_{ij}} \right)}_{p\times r}}$，其中$r$是$\mathbf{V}$的秩。这样$\underset{1\times r}{\mathop{\mathbf{Y}}}\,:=\left( {{y}_{1}},{{y}_{2}},\cdots ,{{y}_{r}} \right)=x\mathbf{A}$，其中${{y}_{i}}$称为第$i$主成分，${{\lambda }_{i}}$是${{y}_{i}}$的方差，${{{\lambda }_{i}}}/{\sum\limits_{i=1}^{p}{{{\lambda }_{i}}}}\;$称为第$i$个主成分的贡献率。

取前$k$个${{y}_{i}}$作为新的指标，以达到压缩数据、简化分析的目的。一般来说$k$满足${\sum\limits_{i=1}^{k}{{{\lambda }_{i}}}}/{\sum\limits_{i=1}^{p}{{{\lambda }_{i}}}}\;\ge 80\%$即可。

另外，${{a}_{ij}}$称为变量${{x}_{i}}$在主成分${{y}_{j}}$上的载荷。

1.2、从相关矩阵出发

也被称为$\mathbf{R}$主成分分析，好处是可以去掉量纲带来的影响。方法和从协方差矩阵出发是一样的，这里不再赘述仅给出结论。

记$\underset{p\times p}{\mathop{\mathbf{R}}}\,=\left( \frac{\operatorname{cov}\left( {{x}_{i}},{{x}_{j}} \right)}{\sqrt{D\left( {{x}_{i}} \right)}\sqrt{D\left( {{x}_{j}} \right)}} \right)$是$\underset{p\times 1}{\mathop{x}}\,$的相关矩阵，记其特征值分别为${{\lambda }_{1}}\ge {{\lambda }_{2}}\ge \cdots \ge {{\lambda }_{r}}$，取${{a}_{i}}$为对应的特征向量${{v}_{i}}$，${{d}_{i}}={1}/{\sqrt{D\left( {{x}_{i}} \right)}}\;$，$\mathbf{D}=diag\left( {{d}_{1}},{{d}_{2}},\cdots ,{{d}_{p}} \right)$

则$\underset{1\times r}{\mathop{\mathbf{Y}}}\,:=\left( {{y}_{1}},{{y}_{2}},\cdots ,{{y}_{r}} \right)=x\mathbf{DA}$为所求的新指标，即主成分。

2、样本主成分

其实对于统计专业的朋友，只要有了理论，其它就都好说了。因为他们知道各种统计量，但对于非统计专业的熊孩子，还是把协方差矩阵和相关系数矩阵的估计量写明白的好。

每个样本作为一行，将其排列成数据矩阵$\underset{n\times p}{\mathop{\mathbf{X}}}\,=\left( {{x}_{ij}} \right)$，$n$是样本量，$p$是样本的指标数量。令${{\mathbf{X}}^{*}}={{\left( {{x}_{ij}}-\overline{{{x}_{j}}} \right)}_{n\times p}}$，其中$\overline{{{x}_{j}}}=\frac{\sum\limits_{k=1}^{n}{{{x}_{kj}}}}{n}$。

对于协方差矩阵通常有两种估计方式：

极大似然估计：

\[\mathbf{V}=\frac{1}{n}{{\mathbf{X}}^{*T}}{{\mathbf{X}}^{*}}=:{{\left( {{v}_{ij}} \right)}_{p\times p}}\]

其中：${{v}_{ij}}=\frac{1}{n}\sum\limits_{k=1}^{n}{\left( {{x}_{ki}}-\overline{{{x}_{i}}} \right)}\left( {{x}_{kj}}-\overline{{{x}_{i}}} \right)=\frac{1}{n}\left[ \sum\limits_{k=1}^{n}{{{x}_{ki}}{{x}_{kj}}}-\frac{\sum\limits_{k=1}^{n}{{{x}_{ki}}}\sum\limits_{k=1}^{n}{{{x}_{kj}}}}{n} \right]$。

无偏估计：

\[\mathbf{S}=\frac{1}{n-1}{{\mathbf{X}}^{*T}}{{\mathbf{X}}^{*}}=:{{\left( {{s}_{ij}} \right)}_{p\times p}}\]

对相关系数矩阵通常用极大似然估计：

\[\mathbf{R}={{\left( \frac{{{s}_{ij}}}{\sqrt{{{s}_{ii}}}\sqrt{{{s}_{jj}}}} \right)}_{p\times p}}=:{{\left( {{r}_{ij}} \right)}_{p\times p}}\]

其中${{r}_{ij}}=\frac{\sum\limits_{k=1}^{n}{\left( {{x}_{ki}}-\overline{{{x}_{i}}} \right)\left( {{x}_{kj}}-\overline{{{x}_{j}}} \right)}}{\sqrt{\sum\limits_{k=1}^{n}{{{\left( {{x}_{ki}}-\overline{{{x}_{i}}} \right)}^{2}}}}\sqrt{\sum\limits_{k=1}^{n}{{{\left( {{x}_{kj}}-\overline{{{x}_{j}}} \right)}^{2}}}}}$。

之后就是计算特征值和特征向量的事儿了。

在Mathematica中一玩耍一下下

在 Mma 中的主成分分析函数是：PrincipalComponents

默认使用协方差矩阵求解，如果需要用相关系数矩阵需要设置参数：Method -> “Correlation”。

看一个最简单的例子，如下图，在平面上取椭圆的一些点，每点作为一个样本，每个样本有两个指标——横纵坐标。

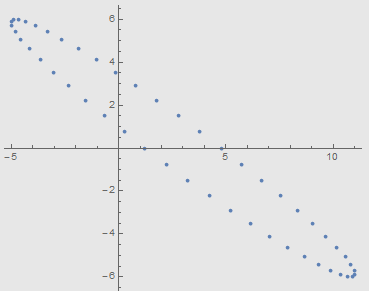
从图中可以看到无论是横坐标还是纵坐标，它们的方差都比较大，也就是说两个指标中都包含了很多信息。而从直观上看，椭圆的长轴才是图形的主要特征。主成分分析就是通过线性变换把数据的主要信息尽可能多地放在前面几个指标中。根据主成分分析方法，对坐标做线性变换后如下图，

可见，横轴几乎包含了数据的所有信息（我还是解释一下“信息”的意思吧。图形的形状在变换前后并没有改变，也就是说变换之后保留了所有原始形状信息。如果想描述某个点的大体位置，在变换后的数据中，只用横的轴数据就可以了。而对于变换之前的数据，只用横轴或只用纵轴都办不到。也就是说，即使删掉变换之后的纵轴数据，只用横轴数据也能保留原始图形形状的绝大部分信息）。

直接使用Mma的内置函数：

da = Table[{8 Cos[2 Pi k/50. + 3 Pi/7] + 3, 6 Sin[2 Pi k/50.]}, {k, 1,
50}];
ListPlot[da, AspectRatio -> Automatic](*图－原数据*)
ListPlot[PrincipalComponents[da], AspectRatio -> Automatic](*图－主成分*)

使用理论方法：

da = Table[{8 Cos[2 Pi k/50. + 3 Pi/7] + 3, 6 Sin[2 Pi k/50.]}, {k, 1,
50}];
ListPlot[da, AspectRatio -> Automatic](*图－原数据*)
{la, v} = Eigensystem[Covariance[da]];(*协方差的特征与对应的单位化特征向量的转置*)
ListPlot[(# - Mean[da] & /@ da).Transpose[v],
AspectRatio -> Automatic](*已平移*)

看一看Mma帮助中的例子

Mma的帮助总是那么销魂，主成分既是飞机的正方向

参考资料

张尧庭,方开泰.《多元统计分析引论》,武汉大学出版社,2013.11.ISBN:9787307119345

王静龙.《多元统计分析》.科学出版社,2008.6.ISBN:9787030215550