题目
在漆黑的夜里,四位旅行者来到了一座狭窄而且没有护栏的桥边。如果不借助手电筒的话,大家是无论如何也不敢过桥去的。不幸的是,四个人一共只带了一只手电筒,而桥窄得只够让两个人同时通过。如果各自单独过桥的话,四人所需要的时间分别是1,2,5,8分钟;而如果两人同时过桥,所需要的时间就是走得比较慢的那个人单独行动时所需的时间。问题是,你如何设计一个方案,让用的时间最少。
这个题目被微软、GOOGLE、百度、华硕、建设银行等很多公司用作笔试题或面试题。当然也有用在IQ测试中。
解法一
解题思路:耗时最少的人去传递手电筒,耗时最多的人两人结伴而行。
为方便叙述答案,在花括号内用每人单独过桥时间表示尚未过桥的人。
最短耗时:15分钟。共有以下两种方案。
方案1:{1,2,5,8}>{5,8}>{2,5,8}>{2}>{1,2}>{空}
方案2:{1,2,5,8}>{5,8}>{1,5,8}>{1}>{1,2}>{空}
此题用Mathematica求解比较方便,代码如下:
用Mathematica穷举
定义函数与穷举
left0 = {1, 2, 5,
8};(*初始桥左侧数据(记桥两端分别为左右),至少有2人要过桥,数据格式:{A的过桥时间,B的过桥时间,C的过桥时间,\
\[Ellipsis]\[Ellipsis]}*)
nGoBack = Length[left0] - 2;(*需要的往返次数*)
left0 = {{0}}~Join~left0;(*在数据前面加上过桥次数标记*)
k = 0;(*往+返次数,奇数为返*)
f[left_] :=
Module[{nleft = Subsets[left[[2 ;;]], {Length[left] - 2 - 1}], ls},
Flatten[{{{k}}~Join~left[[2 ;;]] -> {{k + 1}}~Join~# & /@ nleft,
Flatten[{{k + 1}}~Join~ls -> {{k + 2}}~Join~Union[ls, #] & /@
Subsets[Complement[left0[[2 ;;]], ls = #], {1}] & /@ nleft,
1]}, 1]](*往返一次后所有可能的变化*)
ff[last_] :=
Union[Flatten[k += 2;
f /@ Union[Select[last, OddQ[#[[1]][[1, 1]]] &][[;; , 2]][[2 ;;]]],
1]](*重复执行f*)
goBackData =
Flatten[NestList[ff, f[left0], nGoBack], 1];(*计算所有人过桥后,所有可能的变化*)
goBackData =
Select[goBackData, Length[#[[1]]] > 1 &];(*删除掉最后多余的一次返回数据*)
计算路径与绘图
goBackDataStr = {StringRiffle[ToString /@ Flatten[#[[1]]], ","] ->
StringRiffle[ToString /@ Flatten[#[[2]]], ","],
Max[Flatten[{Complement[#[[1, 2 ;;]], #[[2, 2 ;;]]],
Complement[#[[2, 2 ;;]], #[[1, 2 ;;]]]}]]} & /@
goBackData;(*往返数据字符化,以及过桥用时*)
k = 0;
rule = Flatten[{# -> k++} & /@
DeleteDuplicates[
Flatten[{#[[1]], #[[2]]} & /@
goBackDataStr[[;; , 1]]]]];(*字符串与数字对应规则*)
goBackDataStrSimplify =
goBackDataStr /. rule;(*往返数据简化版,方便在函数FindPath中使用*)
am = AdjacencyMatrix[
goBackDataStrSimplify[[;; , 1]]];(*邻接矩阵,在这里虽然没有用到,但在进一步分析时还是有些作用的*)
allPath =
FindPath[goBackDataStrSimplify[[;; , 1]], 0, Length[rule] - 1,
Infinity, All];(*查找所有从起点到终点的路径*)
bs = Total /@ (Table[#[[k]] -> #[[k + 1]], {k, Length[#] - 1}] & /@
allPath) /. (#[[1]] -> #[[2]] & /@
goBackDataStrSimplify);(*计算每条路径耗时*)
eds = allPath[[First[Ordering[bs]]]];(*最短的路径*)
minTime = Min[bs];(*最短用时*)
"最短过桥方案(花括号内为桥左侧状态):" <>
StringRiffle[
eds /. (#[[2]] ->
If[StringLength[#[[1]]] == 1, "空", StringDrop[#[[1]], 2]] & /@
rule), {"{", "}>{", "}"}]
"最短用时:" <> ToString[minTime](*最短用时*)
edsRule =
Table[(eds[[k]] -> eds[[k + 1]]), {k,
Length[eds] - 1}];(*为方便绘图定义此变量*)
panelLabel[lbl_] :=
Panel[Style[lbl, Bold, 14, FontFamily -> "微软雅黑"], FrameMargins -> 0,
Background -> Lighter[Blue, 0.7]];(*为方便绘图定义此函数*)
layout = ToExpression /@
Flatten[StringCases[#, x : RegularExpression["^\\d+"] :> x] & /@
rule[[;; , 1]]];(*节点所在层,取纵坐标*)
coordinates =
Table[{Count[layout[[;; k]], layout[[k]]] -
Count[layout, layout[[k]]]/2, -layout[[k]]}, {k,
Length[layout]}];(*节点坐标*)
vertexLabels =
Table[i ->
Placed[StringReplace[rule[[i + 1, 1]],
RegularExpression["^\\d+,"] -> ""], Center, panelLabel], {i, 0,
Length[rule] - 1}];(*节点标签*)
edgeStyle =
Table[(eds[[k]] -> eds[[k + 1]]) ->
Directive[Red, Thickness[0.003]], {k, Length[eds] - 1}];(*边样式*)
edgeLabels = #[[1]] ->
Placed[Panel[#[[2]], FrameMargins -> 0], Center] & /@
Select[goBackDataStrSimplify,
MemberQ[edsRule, #[[1]]] &];(*边的标签*)
Graph[goBackDataStrSimplify[[;; , 1]], VertexLabels -> vertexLabels,
EdgeStyle -> edgeStyle, EdgeLabels -> edgeLabels,
VertexCoordinates -> coordinates,
EdgeShapeFunction ->
GraphElementData["FilledArcArrow",
"ArrowSize" ->
0.015]](*绘图,设置这么多参数主要是为了绘置更多人的情况还按此样式绘图,也可以用函数LayeredGraphPlot*)
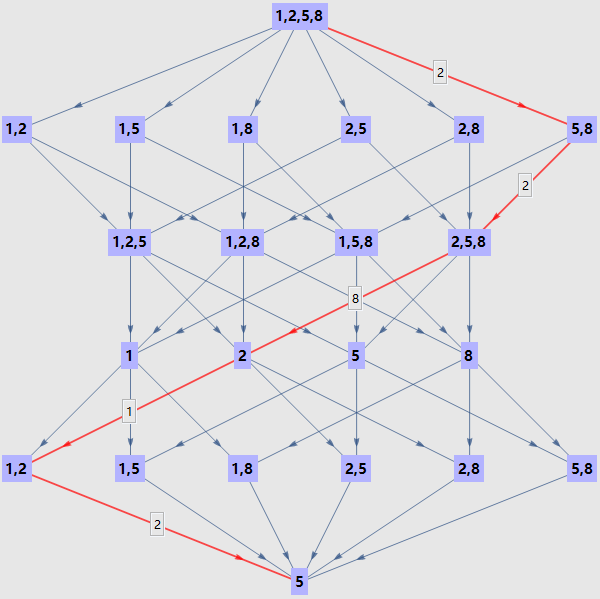
过程图(其中一种方案)
5人过桥
以上程序可以求解多人(大于1)过桥问题。以5人为例,设每人过桥时间:1,2,5,8,13。
最短用时:26分钟。共有8种方案:
- {1,2,5,8,13}>{5,8,13}>{2,5,8,13}>{2,5}>{1,2,5}>{5}>{1,5}>{空}
- {1,2,5,8,13}>{5,8,13}>{2,5,8,13}>{2,5}>{1,2,5}>{2}>{1,2}>{空}
- {1,2,5,8,13}>{5,8,13}>{1,5,8,13}>{8,13}>{2,8,13}>{2}>{1,2}>{空}
- {1,2,5,8,13}>{5,8,13}>{1,5,8,13}>{8,13}>{1,8,13}>{1}>{1,2}>{空}
- {1,2,5,8,13}>{5,8,13}>{1,5,8,13}>{1,5}>{1,2,5}>{5}>{1,5}>{空}
- {1,2,5,8,13}>{5,8,13}>{1,5,8,13}>{1,5}>{1,2,5}>{2}>{1,2}>{空}
- {1,2,5,8,13}>{2,8,13}>{1,2,8,13}>{8,13}>{2,8,13}>{2}>{1,2}>{空}
- {1,2,5,8,13}>{2,8,13}>{1,2,8,13}>{8,13}>{1,8,13}>{1}>{1,2}>{空}
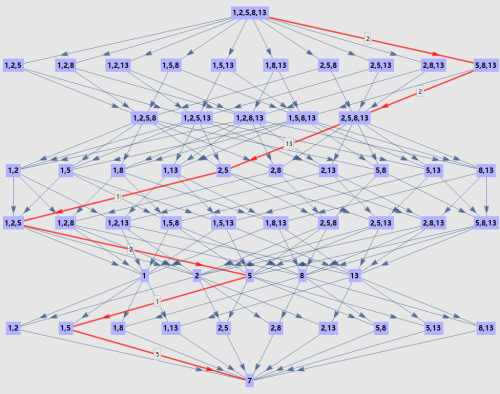
过程图(第1种方案)
2016-04-14
解法二
实际上,此问题可以转化为最短路径问题,用图论方法求解(Mathematica内置了很多图论函数)。核心就是构造以过桥各状态为节点的临接矩阵,然后使用FindShortestPath函数查找最短路径。下面还以4个人,用时分别为:1,2,5,8 为例。
这里把桥两头的状态都放在一个矩阵里,类似于国际象棋的棋盘那样,间隔排列,桥左边的状态只占黑色,桥右边的状态只占白色,状态转移时,只允许从白入黑或黑入白(值为转移时间),不允许同色转移(值为无穷大)。
代码如下:
Remove["Global`*"];
allStatus = Reverse[Subsets[{1, 2, 5, 8}]];
list = Riffle[allStatus, allStatus];
n = Length[list];
f[x_, y_] := Max[Complement[list[[x]], list[[y]]]];(*过桥时间*)
goTo[x_, y_] :=
OddQ[x] && EvenQ[y] && Length[list[[x]]] - Length[list[[y]]] == 2 &&
SubsetQ[list[[x]], list[[y]]];(*判断过桥*)
goBack[x_, y_] :=
EvenQ[x] && OddQ[y] && Length[list[[y]]] - Length[list[[x]]] == 1 &&
SubsetQ[list[[y]], list[[x]]];(*判断返回*)
m = Table[
If[goTo[x, y], f[x, y], If[goBack[x, y], f[y, x], Infinity]], {x,
n}, {y, n}];(*过桥临接矩阵*)
v = FindShortestPath[WeightedAdjacencyGraph[m], 1, n];
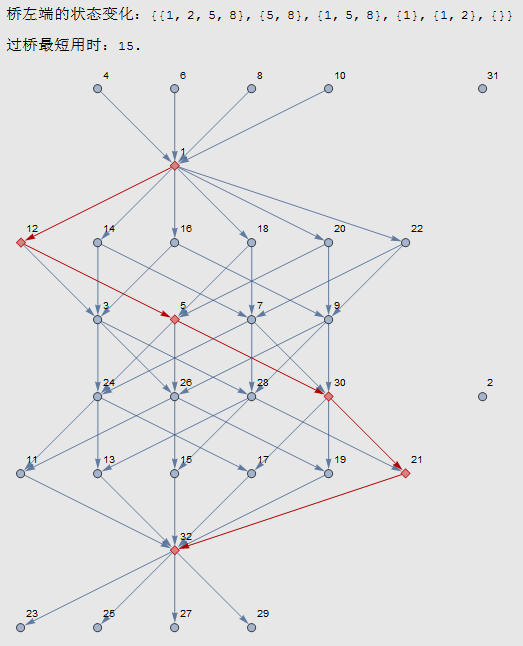
Row[{"桥左端的状态变化:", list[[#]] & /@ v}]
Row[{"过桥最短用时:", GraphDistance[WeightedAdjacencyGraph[m], 1, n]}]
WeightedAdjacencyGraph[m, VertexLabels -> "Name",
GraphHighlight ->
Flatten[{v, #[[1]] -> #[[2]] & /@ Partition[v, 2, 1]}],
GraphHighlightStyle -> {"Thick", "VertexDiamond"}](*绘图*)
输出结果: