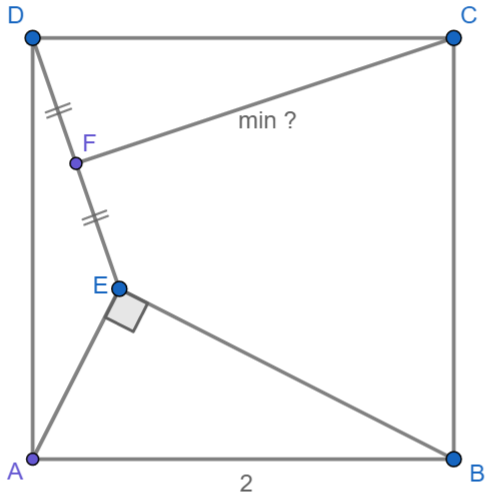
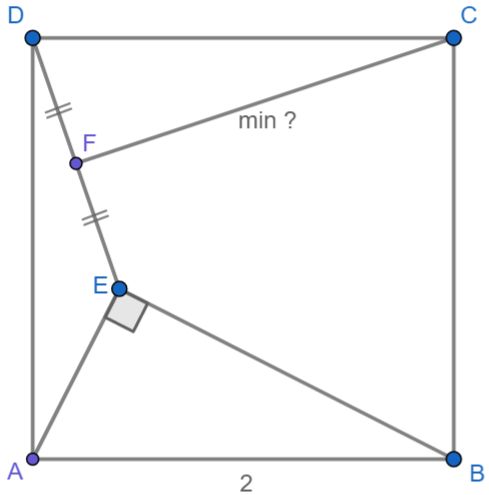
如上图所示。
已知:正方形ABCD的边长为2,点E是正方形内的动点,且满足AE⊥BE,连结DE,点F为线段DE的中点。
求:线段CF的最短长度。
答案:$(\sqrt{13}-1)/2$
1. 描述形式的做法
实际上此题很容易求解,计算过程并不复杂,但要对中间步骤进行严格证明还是比较繁琐的。
下面先说一下大体思路:
易知,点E的轨迹是以AB为直径的半圆;
由相似知识,当点E滑过半圆时,点F的轨迹也是一个半圆(直径为1,直径的端点分别为AD的中点和BD的中点);
所以,当CF的沿长线过小圆的圆心时,CF最短,用勾股定理即可计算出它的长度。
2. 严格形式的做法
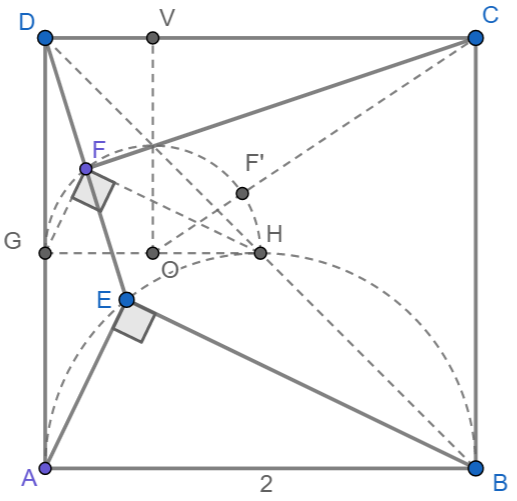
作线段AD的中点G,线段BD的中点H,线段GH的中点O,连结上该连结的线,如上图所示。
∵ 点GF是三角形ADE的中线,
∴ GF//AE,同理有 FH//EB
∴ GF⊥FH
∴ 点F在以GH为直径的半圆上
∴ 线段CF的沿长线过圆心O里,线段CF最短,即图中的CF’
$$\begin{aligned}
CF’&=CO-OF’\\
&=\sqrt{OV^2+CV^2}-OF’\\
&=\sqrt{1^2+(\frac{3}{2})^2}-\frac{1}{2}\\
&={\color{Blue}{\frac{\sqrt{13}-1}{2}}}
\end{aligned}$$
